
| A. | (1+x)2=2000 | B. | 2000(1+x)2=3600 | ||
| C. | (3600-2000)(1+x)=3600 | D. | (3600-2000)(1+x)2=3600 |
科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(文)试卷(解析版) 题型:选择题
设数列{an}满足a1+2a2=3,且对任意的n∈N*,点Pn(n,an)都有向量PnPn+1=(1,2),则{an}的前n项和Sn为( )
A.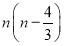 B.
B.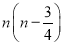
C.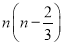 D.
D.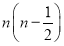
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7米/秒 | B. | 6米/秒 | C. | 5米/秒 | D. | 8米/秒 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6x-y-18=0 | B. | 8x-y-24=0 | C. | 5x-2y-15=0 | D. | 8x-3y-24=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
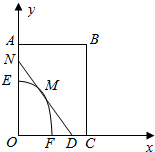 如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.
如图,某小区有一矩形地块OABC,其中OC=2,OA=3,单位:百米.已知 O EF是一个游泳池,计划在地块OABC内修一条与池边 EF相切于点 M的直路l(宽度不计),交线段OC于点D,交线段OA于点 N.现以点 O为坐标原点,以线段 OC所在直线为x轴,建立平面直角坐标系,若池边 EF满足函数y=-x2+2($0≤x≤\sqrt{2}$)的图象.若点 M到y轴距离记为t.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com