
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
. |
| x |
| 10+20+30+40+50+60+70+80 |
| 8 |
. |
| y |
| 62+68+75+81+89+95+102+108 |
| 8 |
| 8 |
 |
| i=1 |
| 8 |
 |
| i=1 |
| x | 2 i |
. |
| x |
. |
| x |
. |
| y |
| 33400-30600 |
| 20400-16200 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
| 实验顺序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 67 | 75 | 80 | 89 |
| ? |
| y |
| ? |
| b |
| ? |
| a |
查看答案和解析>>
科目:高中数学 来源: 题型:
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| 实验顺序 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(分钟) | 62 | 67 | 75 | 80 | 89 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
 |
| b |
. |
| x |
. |
| x |
| 1 |
| n |
| n |
 |
| t=1 |
. |
| y |
| n |
 |
| t=1 |
查看答案和解析>>
科目:高中数学 来源:2014届湖北武汉部分重点中学高二上学期期末考试文科数学卷(解析版) 题型:选择题
一个车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了8次试验,收集数据如下:
|
零件个数x(个) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
加工时间y(分钟) |
62 |
68 |
75 |
81 |
89 |
95 |
102 |
108 |
设回归直线方程为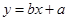 ,则点
,则点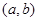 在直线
在直线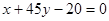 的( )
的( )
A、右上方 B、右下方 C、左上方 D、左下方
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com