
分析 (1)该函数是由y=$\frac{1}{2}sint$和t=$\frac{π}{4}-2x$复合而成的复合函数,函数$t=\frac{π}{4}-2x$为减函数,从而使y=$\frac{1}{2}sint$为增函数的x所在区间便是原函数的单调减区间,使y=$\frac{1}{2}$sint为减函数的x所在区间便是原函数的单调增区间,这样根据正弦函数的单调区间便可得出原函数的单调增、减区间;
(2)和(1)同样的方法,根据复合函数的单调性及余弦函数的单调区间便可得出原函数的单调区间.
解答 解:(1)解$-\frac{π}{2}+2kπ≤\frac{π}{4}-2x≤\frac{π}{2}+2kπ$,k∈Z得:$-\frac{π}{8}-kπ≤x≤\frac{3π}{8}-kπ,k∈Z$;
∴该函数的单调递减区间为$[-\frac{π}{8}-kπ,\frac{3π}{8}-kπ]$,k∈Z;
解$\frac{π}{2}+2kπ≤\frac{π}{4}-2x≤\frac{3π}{2}+2kπ$,k∈Z得:$-\frac{5π}{8}-kπ≤x≤-\frac{π}{8}-kπ,k∈Z$;
∴该函数的单调递增区间为[$-\frac{5π}{8}-kπ,-\frac{π}{8}-kπ$],k∈Z;
(2)解-π+2kπ≤2x≤2kπ得,$-\frac{π}{2}+kπ≤x≤kπ$,k∈Z;
解2kπ≤2x≤π+2kπ得,$kπ≤x≤\frac{π}{2}+kπ$,k∈Z;
∴该函数的单调递增区间为$[-\frac{π}{2}+kπ,kπ],k∈Z$;
单调递减区间为[kπ,$\frac{π}{2}+kπ$],k∈Z.
点评 考查复合函数的定义,以及复合函数的单调性的判断及单调区间的求法,正弦函数和余弦函数的单调区间,一次函数的单调性.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{ON}$ | B. | $\overrightarrow{AM}$ | C. | $\overrightarrow{AN}$ | D. | 2$\overrightarrow{AN}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
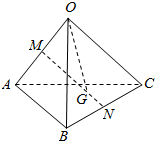 如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.
如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com