
【题目】已知不等式![]() 的解集为
的解集为![]() 或
或![]() .
.
(1)求![]() ;(2)解关于
;(2)解关于![]() 的不等式
的不等式![]()
【答案】(1)a=1,b=2;(2)①当c>2时,解集为{x|2<x<c};②当c<2时,解集为{x|c<x<2};③当c=2时,解集为.
【解析】
(1)根据不等式ax2﹣3x+6>4的解集,利用根与系数的关系,求得a、b的值;
(2)把不等式ax2﹣(ac+b)x+bc<0化为x2﹣(2+c)x+2c<0,讨论c的取值,求出对应不等式的解集.
(1)因为不等式ax2﹣3x+6>4的解集为{x|x<1,或x>b},
所以1和b是方程ax2﹣3x+2=0的两个实数根,且b>1;
由根与系数的关系,得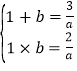 ,
,
解得a=1,b=2;
(2)所求不等式ax2﹣(ac+b)x+bc<0化为x2﹣(2+c)x+2c<0,
即(x﹣2)(x﹣c)<0;
①当c>2时,不等式(x﹣2)(x﹣c)<0的解集为{x|2<x<c};
②当c<2时,不等式(x﹣2)(x﹣c)<0的解集为{x|c<x<2};
③当c=2时,不等式(x﹣2)(x﹣c)<0的解集为.


科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C1的方程为ρsin(θ+ ![]() )+2
)+2 ![]() =0,曲线C2的参数方程为
=0,曲线C2的参数方程为 ![]() (θ为参数).
(θ为参数).
(1)将C1的方程化为直角坐标方程;
(2)若点Q为C2上的动点,P为C1上的动点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在我国古代数学名著《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”.已知三棱维![]() 中,
中,![]() 底面
底面![]() .
.

(1)从三棱锥![]() 中选择合适的两条棱填空_________⊥________,则该三棱锥为“鳖臑”;
中选择合适的两条棱填空_________⊥________,则该三棱锥为“鳖臑”;
(2)如图,已知![]() 垂足为
垂足为![]() ,垂足为
,垂足为![]() .
.
(i)证明:平面![]() ⊥平面
⊥平面![]() ;
;
(ii)作出平面![]() 与平面
与平面![]() 的交线
的交线![]() ,并证明
,并证明![]() 是二面角
是二面角![]() 的平面角.(在图中体现作图过程不必写出画法)
的平面角.(在图中体现作图过程不必写出画法)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年电子商务蓬勃发展,平台对每次成功交易都有针对商品和快递是否满意的评价系统.从该评价系统中选出200次成功交易,并对其评价进行统计,网购者对商品的满意率为0.70,对快递的满意率为0.60,商品和快递都满意的交易为80
(Ⅰ)根据已知条件完成下面的![]() 列联表,并回答能否有99%认为“网购者对商品满意与对快递满意之间有关系”?
列联表,并回答能否有99%认为“网购者对商品满意与对快递满意之间有关系”?
对快递满意 | 对快递不满意 | 合计 | |
对商品满意 | 80 | ||
对商品不满意 | |||
合计 | 200 |
(Ⅱ)若将频率视为概率,某人在该网购平台上进行的3次购物中,设对商品和快递都满意的次数为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
附:![]() ,
,
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化,某调查机构随机抽取10名购物者进行采访,5名男性购物者中有3名倾向于选择网购,2名倾向于选择实体店,5名女性购物者中有2名倾向于选择网购,3名倾向于选择实体店.
(1)若从10名购物者中随机抽取2名,其中男、女各一名,求至少1名倾向于选择实体店的概率;
(2)若从这10名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(2x+φ),其中φ为实数,若f(x)≤|f( ![]() )|对x∈R恒成立,且f(
)|对x∈R恒成立,且f( ![]() )>f(π),则f(x)的单调递增区间是( )
)>f(π),则f(x)的单调递增区间是( )
A.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
B.[kπ,kπ+ ![]() ](k∈Z)
](k∈Z)
C.[kπ+ ![]() ,kπ+
,kπ+ ![]() ](k∈Z)
](k∈Z)
D.[kπ﹣ ![]() ,kπ](k∈Z)
,kπ](k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.
(Ⅰ)求证:BC⊥平面ACFE;
(Ⅱ)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】手机支付也称为移动支付![]() ,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
,是指允许移动用户使用其移动终端(通常是手机)对所消费的商品或服务进行账务支付的一种服务方式.继卡类支付、网络支付后,手机支付俨然成为新宠.某金融机构为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有100个人,把这100个人按照年龄分成5组,然后绘制成如图所示的频率分布表和频率分布直方图.
组数 | 第l组 | 第2组 | 第3组 | 第4组 | 第5组 |
分组 |
|
|
|
|
|
频数 | 20 | 36 | 30 | 10 | 4 |

(1)求![]() ;
;
(2)从第l,3,4组中用分层抽样的方法抽取6人,求第l,3,4组抽取的人数:
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某精密仪器生产有两道相互独立的先后工序,每道工序都要经过相互独立的工序检查,且当第一道工序检查合格后才能进入第二道工序,两道工序都合格,产品才完全合格,.经长期监测发现,该仪器第一道工序检查合格的概率为 ![]() ,第二道工序检查合格的概率为
,第二道工序检查合格的概率为 ![]() ,已知该厂三个生产小组分别每月负责生产一台这种仪器.
,已知该厂三个生产小组分别每月负责生产一台这种仪器.
(1)求本月恰有两台仪器完全合格的概率;
(2)若生产一台仪器合格可盈利5万元,不合格则要亏损1万元,记该厂每月的赢利额为ξ,求ξ的分布列和每月的盈利期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com