
【题目】已知集合![]()
(1)判断8,9,10是否属于集合![]() ;
;
(2)已知集合![]() ,证明:“
,证明:“![]() ”的充分非必要条件是“
”的充分非必要条件是“![]() ”;
”;
(3)写出所有满足集合![]() 的偶数.
的偶数.
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)详见解析;(3)所有满足集合
;(2)详见解析;(3)所有满足集合![]() 的偶数为
的偶数为![]() ,
,![]() .
.
【解析】
(1)将![]() ,
,![]() ,
,![]() 分别代入关系式
分别代入关系式![]() ,若满足关系式,则属于
,若满足关系式,则属于![]() ,若不满足关系式,则不属于
,若不满足关系式,则不属于![]() ,即可得答案;
,即可得答案;
(2)根据已知中集合![]() 的定义,根据集合元素与集合关系的判断,我们推证奇数
的定义,根据集合元素与集合关系的判断,我们推证奇数![]() 可得答案;
可得答案;
(3)![]() 成立,当
成立,当![]() ,
,![]() 同奇或同偶时,
同奇或同偶时,![]() ,
,![]() 均为偶数;当
均为偶数;当![]() ,
,![]() 一奇,一偶时,
一奇,一偶时,![]() ,
,![]() 均为奇数.由此能求出所有满足集合
均为奇数.由此能求出所有满足集合![]() 的偶数.
的偶数.
(1)![]()
![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,
假设![]() ,
,![]() ,则
,则![]() ,且
,且![]() ,
,
![]()
![]() ,
,
![]()
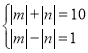 ,或
,或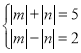 ,显然均无整数解,
,显然均无整数解,
![]()
![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ;
;
(2)![]() 集合
集合![]() ,则恒有
,则恒有![]() ,
,
![]()
![]() ,
,![]() 即一切奇数都属于
即一切奇数都属于![]() ,
,
又![]()
![]() ,
,![]() “
“![]() ”的充分非必要条件是“
”的充分非必要条件是“![]() ”;
”;
(3)集合![]() ,
,![]() 成立,
成立,
①当![]() ,
,![]() 同奇或同偶时,
同奇或同偶时,![]() ,
,![]() 均为偶数,
均为偶数,![]() 为4的倍数;
为4的倍数;
②当![]() ,
,![]() 一奇,一偶时,
一奇,一偶时,![]() ,
,![]() 均为奇数,
均为奇数,![]() 为奇数,
为奇数,
综上所有满足集合![]() 的偶数为
的偶数为![]() ,
,![]() .
.


科目:高中数学 来源: 题型:
【题目】为推动文明城市创建,提升城市整体形象,2018年12月30日盐城市人民政府出台了《盐城市停车管理办法》,2019年3月1日起施行.这项工作有利于市民养成良好的停车习惯,帮助他们树立绿色出行的意识,受到了广大市民的一致好评.现从某单位随机抽取80名职工,统计了他们一周内路边停车的时间t(单位:小时),整理得到数据分组及频率分布直方图如下:


(1)从该单位随机选取一名职工,试估计这名职工一周内路边停车的时间少于8小时的概率;
(2)求频率分布直方图中a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() ;对任意的
;对任意的![]() 、
、![]() ,
,![]() ,与
,与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)当![]() 时,若
时,若![]() ,求集合
,求集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业有2个分厂生产某种零件,为了研究两个分厂生产零件的质量是否有差异,随机从2个分厂生产的零件中各抽取了500件,具体数据如下表所示:
甲厂 | 乙厂 | 总计 | |
优质品 | 360 | 320 | 680 |
非优质品 | 140 | 180 | 320 |
总计 | 500 | 500 | 1000 |
根据表中数据得![]() 的观测值
的观测值![]() ,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A.0.1B.0.01C.0.05D.0.001
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年开始,国家逐步推行全新的高考制度.新高考不再分文理科,采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生 450 人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含女生45人,求
名学生中含女生45人,求![]() 的值及抽取到的男生人数;
的值及抽取到的男生人数;
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的![]() 列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取的选择“地理”的学生中按分层抽样再抽取6名,再从这6名学生中抽取2人了解学生对“地理”的选课意向情况,求2人中至少有1名男生的概率.

| 0.05 | 0.01 |
| 3.841 | 6.635 |
参考公式:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在
在![]() 时有最大值
时有最大值![]() 和最小值
和最小值![]() ,设
,设![]() .
.
(1)求实数![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com