
| A. | (0,$\frac{1}{4}$) | B. | [$\frac{1}{4}$,1) | C. | ($\frac{1}{16}$,1) | D. | [$\frac{1}{16}$,1) |
分析 不等式${x^2}-{log_m}^x<0(m>0$且m≠1)在(0,$\frac{1}{2}$)内恒成立?${lo{g}_{m}}^{x}$>x2在(0,$\frac{1}{2}$)内恒成立,利用对数函数的单调性可得${lo{g}_{m}}^{\frac{1}{2}}$≥${(\frac{1}{2})}^{2}$=$\frac{1}{4}$,继而可求得实数 m 的取值范围.
解答 解:∵${x^2}-{log_m}^x<0(m>0$且m≠1)在(0,$\frac{1}{2}$)内恒成立,
∴${lo{g}_{m}}^{x}$>x2在(0,$\frac{1}{2}$)内恒成立,∴0<m<1,
且${lo{g}_{m}}^{\frac{1}{2}}$≥${(\frac{1}{2})}^{2}$=$\frac{1}{4}$,
∴${m}^{\frac{1}{4}}$≥$\frac{1}{2}$,
∴m≥$\frac{1}{16}$,又0<m<1,
∴实数 m 的取值范围为[$\frac{1}{16}$,1).
故选:D.
点评 本题考查函数恒成立问题,考查对数函数的单调性质的理解与应用,得到${lo{g}_{m}}^{\frac{1}{2}}$≥${(\frac{1}{2})}^{2}$=$\frac{1}{4}$是关键,属于中档题.


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 16 | 14 | 12 | 8 |
| 每小时生产有 缺点的零件数y(件) | 11 | 9 | 8 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
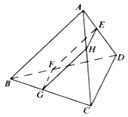 如图,在四面体ABCD中,AB=CD=2,AB与CD所成的角为45°,点E,F,G,H分别在棱EC,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是1.
如图,在四面体ABCD中,AB=CD=2,AB与CD所成的角为45°,点E,F,G,H分别在棱EC,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com