【题目】若不等式m2﹣2km≥0对所有k∈[﹣1，1]恒成立，则实数m的取值范围是______.
【答案】（﹣∞，﹣2]∪{0}∪[2，+∞）
【解析】
首先题目所给条件是关于k的不等式恒成立，求m的范围；其次可以将不等式的左半部分看作是关于k的一次函数，此时问题转化为在某一区间函数值≥0恒成立，所以我们可以用分离参数法解决此问题．
解：令y=m2﹣2km，则有y≥0对k∈[﹣1，1]恒成立，
不等式m2﹣2km≥02km≤m2，
依题意关于k的不等式解集为[﹣1，1]，所以分以下几种情况：
①当m=0时，不等式为0≤0成立；
②当m＞0时，不等式的解为
，只需满足条件
即可，此时m≥2；
③当m＜0时，不等式的解为
，只需满足条件
即可，此时m≤﹣2；
故答案为：（﹣∞，﹣2]∪{0}∪[2，+∞）．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】质检部门从某超市销售的甲、乙两种食用油中分别随机抽取100桶检测某项质量指标，由检测结果得到如图的频率分布直方图：
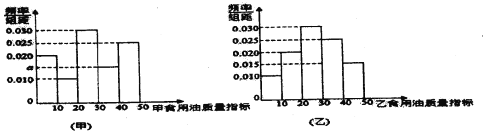
(I)写出频率分布直方图(甲）中
的值；记甲、乙两种食用油100桶样本的质量指标的方差分别为
，试比较的大小（只要求写出答案）；
(Ⅱ)佑计在甲、乙两种食用油中各随机抽取1桶，恰有一个桶的质量指标大于20，且另—个桶的质量指标不大于20的概率；
(Ⅲ)由频率分布直方图可以认为，乙种食用油的质量指标值
服从正态分布
.其中
近似为样本平均数
，
近似为样本方差
，设
表示从乙种食用油中随机抽取10桶，其质量指标值位于（14.55， 38.45)的桶数，求的数学期望.
注：①同一组数据用该区间的中点值作代表，计算得
：
②若
，则
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．
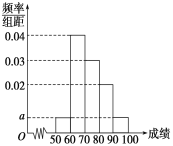
(1)求图中a的值；
(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某技校开展技能大赛，甲、乙两班各选取5名学生加工某种零件，在4个小时内每名学生加工的合格零件数的统计数据的茎叶图如图所示，已知甲班学生在4个小时内加工的合格零件数的平均数为21，乙班学生在4个小时内加工的合格零件数的平均数不低于甲班的平均数.
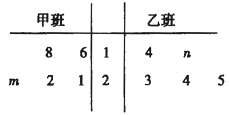
（1）求
的值；
（2）分别求出甲、乙两班学生在4个小时内加工的合格零件数的方差
和
，并由此比较两班学生的加工水平的稳定性.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的离心率为
，抛物线
与椭圆
在第一线象限的交点为
．
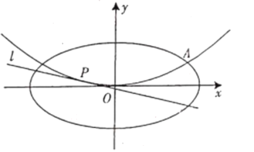
（1）求曲线、
的方程；
（2）在抛物线上任取一点
，在点处作抛物线的切线
，若椭圆上存在两点关于直线对称，求点的纵坐标的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
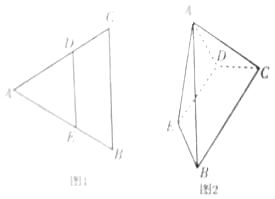
【题目】如图1，等边△ABC中，AC＝4，D是边AC上的点（不与A，C重合），过点D作DE∥BC交AB于点E，沿DE将△ADE向上折起，使得平面ADE⊥平面BCDE，如图2所示．
（1）若异面直线BE与AC垂直，确定图1中点D的位置；
（2）证明：无论点D的位置如何，二面角D﹣AE﹣B的余弦值都为定值，并求出这个定值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
