
【题目】以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知曲线C1的参数方程为 ![]() ,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
,(α为参数,且α∈[0,π]),曲线C2的极坐标方程为ρ=﹣2sinθ.
(Ⅰ)求C1的极坐标方程与C2的直角坐标方程;
(Ⅱ)若P是C1上任意一点,过点P的直线l交C2于点M,N,求|PM||PN|的取值范围.
【答案】解:(1)消去参数可得x2+y2=1,由α∈[0,π),则﹣1x1,0y1, ∴曲线C1是x2+y2=1在x轴上方的部分,
∴曲线C1的极坐标方程为ρ=1(0θπ).
曲线C2的直角坐标方程为x2+(y+1)2=1;
(Ⅱ)设P(x0 , y2),则0y01,直线l的倾斜角为α,
则直线l的参数方程为:{x=x0+tcosαy=y0+tsinα}(t为参数).
代入C2的直角坐标方程得(x0+tcosα)2+(y0+tsinα+1)2=1,
由直线参数方程中t的几何意义可知|PM||PN|=|1+2y0|,
因为0y21,
∴|PM||PN|=∈[1,3]
【解析】(1)求出C1的普通方程,即可求C1的极坐标方程,利用极坐标方程与直角坐标方程的互化方法得出C2的直角坐标方程;(2)直线l的参数方程,代入C2的直角坐标方程得(x0+tcosα)2+(y0+tsinα+1)2=1,由直线参数方程中t的几何意义可知|PM||PN|=|1+2y0|,即可求|PM||PN|的取值范围.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆的离心率e= ![]() ,左、右焦点分别为F1、F2 , 定点,P(2,
,左、右焦点分别为F1、F2 , 定点,P(2, ![]() ),点F2在线段PF1的中垂线上.
),点F2在线段PF1的中垂线上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l:y=kx+m与椭圆C交于M、N两点,直线F2M、F2N的倾斜角分别为α、β且α+β=π,求证:直线l过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,角A,B,C的对边分别为a,b,c,且三角形的面积S= ![]() accosB.
accosB.
(1)求角B的大小;
(2)若a=2 ![]() ,点D在AB的延长线上,且AD=3,cos∠ADC=
,点D在AB的延长线上,且AD=3,cos∠ADC= ![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】牛顿法求方程f(x)=0近似根原理如下:求函数y=f(x)在点(xn , f(xn))处的切线y=f′(xn)(x﹣xn)+f(xn),其与x轴交点横坐标xn+1=xn﹣ ![]() (n∈N*),则xn+1比xn更靠近f(x)=0的根,现已知f(x)=x2﹣3,求f(x)=0的一个根的程序框图如图所示,则输出的结果为( )
(n∈N*),则xn+1比xn更靠近f(x)=0的根,现已知f(x)=x2﹣3,求f(x)=0的一个根的程序框图如图所示,则输出的结果为( ) 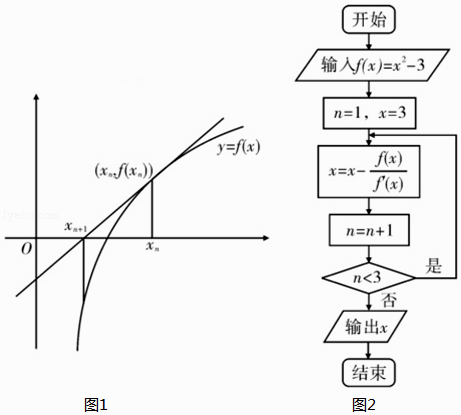
A.2
B.1.75
C.1.732
D.1.73
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 是定义在
是定义在![]() 上的偶函数,且当
上的偶函数,且当![]() 时,
时,![]() .现已画出函数
.现已画出函数![]() 在
在![]() 轴左侧的图象,如图所示,根据图象:
轴左侧的图象,如图所示,根据图象:

(1)请将函数![]() 的图象补充完整并写出该函数的增区间(不用证明).
的图象补充完整并写出该函数的增区间(不用证明).
(2)求函数![]() 的解析式.
的解析式.
(3)若函数![]() ,求函数
,求函数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() +
+ ![]() .
.
(1)求f(x)≥f(4)的解集;
(2)设函数g(x)=k(x﹣3),k∈R,若f(x)>g(x)对任意的x∈R都成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ﹣2cosθ﹣6sinθ+ ![]() =0,直线l的参数方程为
=0,直线l的参数方程为  (t为参数).
(t为参数).
(1)求曲线C的普通方程;
(2)若直线l与曲线C交于A,B两点,点P的坐标为(3,3),求|PA|+|PB|的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com