
【题目】某地区对当地的某种土特产的销售量y(吨)和销售单价x(元/千克)之间的关系进行了调查,得到下表中的数据:
销售单价x(元/千克) | 11 | 10.5 | 10 | 9.5 | 9 | 8 |
销售量y(吨) | 5 | 6 | 8 | 10 | 11 | 14.1 |
(1)根据前5组数据,求出y关于x的回归直线方程.
(2)若由回归直线方程得到的估计数据与剩下的检验数据的误差不超过0.5,则认为回归直线方程是理想的,试问(1)中得到的回归直线方程是否理想?
(3)如果销售量y(吨)和销售单价x(元/千克)之间仍然服从(1)中的关系,进货成本为2.5元/千克,且货源充足(未售完的部分可按成本价全部售出),为了使利润最大,请你就如何确定销售单价给出合理建议.(每千克销售单价不超过12元)
参考公式:回归直线方程![]() ,其中
,其中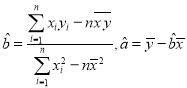 .
.
参考数据:![]() .
.
【答案】(1)![]() ;(2)可以认为该回归直线方程是理想的;(3)将销售单价定为7.5元/千克可使利润最大.
;(2)可以认为该回归直线方程是理想的;(3)将销售单价定为7.5元/千克可使利润最大.
【解析】
(1)由题意计算出![]() 、
、![]() ,代入公式可得
,代入公式可得![]() 、
、![]() ,即可得y关于x的回归直线方程;
,即可得y关于x的回归直线方程;
(2)把![]() 代入回归直线方程可得
代入回归直线方程可得![]() ,再由
,再由![]() 与0.5比较即可得解;
与0.5比较即可得解;
(3)设销售利润为W(千元),由题意可得![]() 关于x的函数表达式,再利用基本不等式即可得解.
关于x的函数表达式,再利用基本不等式即可得解.
(1)因为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以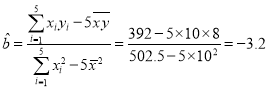 ,
,
所以![]() ,
,
所以y关于x的回归直线方程为![]() ;
;
(2)当![]() 时,
时,![]() ,则
,则![]() ,
,
所以可以认为该回归直线方程是理想的;
(3)设销售利润为W(千元),
因为销售量y(吨)和销售单价x(元/千克)之间满足![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以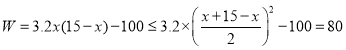 ,
,
当且仅当![]() 即
即![]() 时,W取得最大值,
时,W取得最大值,
所以将销售单价定为7.5元/千克可使利润最大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为![]() (t为参数),直线l2的参数方程为
(t为参数),直线l2的参数方程为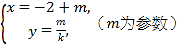 .设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
.设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ) ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的右焦点、右顶点分别为F,A,过原点的直线与椭圆C交于点P、Q(点P在第一象限内),连结PA,QF.若
的右焦点、右顶点分别为F,A,过原点的直线与椭圆C交于点P、Q(点P在第一象限内),连结PA,QF.若![]() ,
,![]() 的面积是
的面积是![]() 面积的3倍.
面积的3倍.
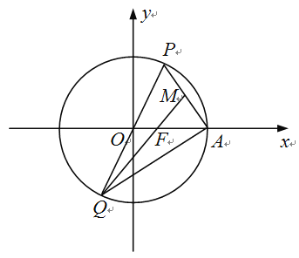
(1)求椭圆C的标准方程;
(2)已知M为线段PA的中点,连结QA,QM.
①求证:Q,F,M三点共线;
②记直线QP,QM,QA的斜率分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学名著《九章算术》中记载:“刍(chú)甍(méng)者,下有袤有广,而上有袤无广.刍,草也.甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱.刍甍字面意思为茅草屋顶.”若刍甍的三视图如图所示,主视图是上底为2,下底为4,高为1的等腰梯形,左视图是底边为2的等腰三角形,则该几何体的体积为( ).
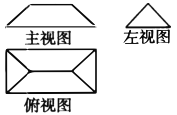
A.![]() B.
B.![]() C.2D.4
C.2D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以坐标原点为极点, ![]() 轴正半轴为极轴,建立极坐标系,点
轴正半轴为极轴,建立极坐标系,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 过点
过点![]() ,曲线
,曲线![]() 的参考方程为
的参考方程为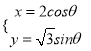 (
(![]() 为参数).
为参数).
(1)求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值与最小值;
的距离的最大值与最小值;
(2)过点![]() 与直线
与直线![]() 平行的直线
平行的直线![]() 与曲
与曲![]() 线交于
线交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,将
的中点,将![]() ,
,![]() 分别沿
分别沿![]() ,
,![]()
向上折起,使![]() ,
,![]() 重合于点
重合于点![]() ,得到三棱锥
,得到三棱锥![]() .试在三棱锥
.试在三棱锥![]() 中,
中,
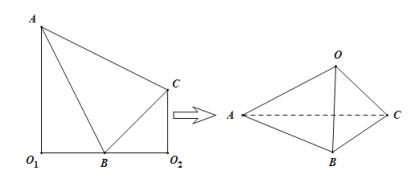
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是首项为1的等差数列,数列
是首项为1的等差数列,数列![]() 是公比不为1的等比数列,且满足
是公比不为1的等比数列,且满足![]() ,
,![]() ,
,![]()
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)令![]() ,记数列
,记数列![]() 的前n项和为
的前n项和为![]() ,求证:对任意的
,求证:对任意的![]() ,都有
,都有![]() ;
;
(3)若数列![]() 满足
满足![]() ,
,![]() ,记
,记![]() ,是否存在整数
,是否存在整数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( )

A.20°B.40°
C.50°D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com