
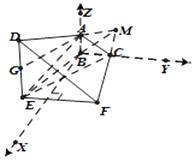
【题目】五面体ABC﹣DEF中,面BCFE是梯形,BC∥EF,面ABED⊥面BCFE,且AB⊥BE,DE⊥BE,AG⊥DE于G,若BE=BC=CF=2,EF=ED=4. 
(1)求证:G是DE中点;
(2)求二面角A﹣CE﹣F的平面角的余弦.
【答案】
(1)证明:延长EB,FC交于M 因为M∈EB,所以M∈面AEBD M∈CF,所以M∈面CFDA
因为面AEBD与面CFDA交于DA 所以M∈DA
因为AB∥DE,BC∥EF 所以 ![]()
由条件,易知四边形ABEG是矩形,所以 ![]()
即G是DE中点
(2)解:作BE⊥EF于E,以 ![]() ,
, ![]() ,
, ![]() 分别为x,y,z轴构建空间直角坐标系,
分别为x,y,z轴构建空间直角坐标系,
所以E( ![]() ,﹣1,0),A(0,0,2),C(O,2,O),令面AEC的法向量为
,﹣1,0),A(0,0,2),C(O,2,O),令面AEC的法向量为 ![]() =(x,y,z),
=(x,y,z),
所以 ![]()
![]() =0;
=0; ![]() =0,易得
=0,易得 ![]() 的一个值为(
的一个值为( ![]() ,1,1),
,1,1),
因为AB垂直面BEFC,所以可令面EFC法向量为 ![]() =(0,0,1)
=(0,0,1)
所以cos ![]() =
= ![]()
所以二面角A﹣EC﹣F的余弦值为 ![]()
【解析】(1)延长EB,FC交于M,可得 M∈DA,由条件,易知四边形ABEG是矩形,所以 ![]() ,即G是DE中点(2)作BE⊥EF于E,以
,即G是DE中点(2)作BE⊥EF于E,以 ![]() ,
, ![]() ,
, ![]() 分别为x,y,z轴构建空间直角坐标系,
分别为x,y,z轴构建空间直角坐标系,
所以E( ![]() ,﹣1,0),A(0,0,2),C(O,2,O),利用向量法求解
,﹣1,0),A(0,0,2),C(O,2,O),利用向量法求解


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】若对圆(x﹣1)2+(y﹣1)2=1上任意一点P(x,y),|3x﹣4y+a|+|3x﹣4y﹣9|的取值与x,y无关,则实数a的取值范围是( )
A.a≤﹣4
B.﹣4≤a≤6
C.a≤﹣4或a≥6
D.a≥6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , a1=1,an+1=λSn+1(n∈N*,λ≠﹣1),且a1、2a2、a3+3成等差数列.
(1)求证:数列{an}为等比数列;
(2)设bn=2an﹣1,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知极点为直角坐标系的原点,极轴为x轴正半轴且单位长度相同的极坐标系中曲线C1:ρ=1,  (t为参数).
(t为参数).
(1)求曲线C1上的点到曲线C2距离的最小值;
(2)若把C1上各点的横坐标都扩大为原来的2倍,纵坐标扩大为原来的 ![]() 倍,得到曲线
倍,得到曲线 ![]() .设P(﹣1,1),曲线C2与
.设P(﹣1,1),曲线C2与 ![]() 交于A,B两点,求|PA|+|PB|.
交于A,B两点,求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|x2﹣2x﹣1|,若a>b>1,且f(a)=f(b),则ab﹣a﹣b的取值范围为( )
A.(﹣2,3)
B.(﹣2,2)
C.(1,2)
D.(﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三角形ABC中,角A,B,C所对边分别为a,b,c,满足(2b﹣c)cosA=acosC.
(1)求角A;
(2)若 ![]() ,b+c=5,求三角形ABC的面积.
,b+c=5,求三角形ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C1:(x+1)2+(y﹣1)2=4,圆C2与圆C1关于直线x﹣y﹣1=0对称,则圆C2的方程为( )
A.(x+2)2+(y﹣2)2=4
B.(x﹣2)2+(y+2)2=4
C.(x+2)2+(y+2)2=4
D.(x﹣2)2+(y﹣2)2=4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(sinx+cosx)+a,g(x)=(a2﹣a+10)ex(a为常数).
(1)已知a=0,求曲线y=f(x)在(0,f(0))处的切线方程;
(2)当0≤x≤π时,求f(x)的值域;
(3)若存在x1、x2∈[0,π],使得|f(x1)﹣g(x2)|<13﹣e ![]() 成立,求实数a的取值范围.
成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的各项均为正数,且an+1=an+ ![]() ﹣1(n∈N*),{an}的前n项和是Sn .
﹣1(n∈N*),{an}的前n项和是Sn .
(Ⅰ)若{an}是递增数列,求a1的取值范围;
(Ⅱ)若a1>2,且对任意n∈N* , 都有Sn≥na1﹣ ![]() (n﹣1),证明:Sn<2n+1.
(n﹣1),证明:Sn<2n+1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com