已知函数f(x)=mx3-x2+nx+13(m、n∈R).
(1)若函数f(x)在x=-2与x=1时取得极值,求m、n的值;
(2)当m=n=0时,若f(x)在闭区间[a,b](a<b)上有最小值4a,最大值4b,求区间[a,b].
解(1)f′(x)=3mx
2-2x+n,由题意知-2和1是方程f′(x)=0的两根,所以-2+1=
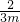
,-2×1=
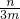
,解得m=-

,n=4.
(2)当m=n=0时,f(x)=-x
2+13.
①若a<b≤0,因为f(x)在[a,b]上单调递增,所以f(a)=4a,f(b)=4b,即
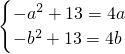
,
所以a,b是方程x
2+4x-13=0的两个不等实根,但此方程两根异号,与a<b≤0矛盾,此时无解;
②若0≤a<b,f(x)在[a,b]上单调递减,
所以f(a)=4b,f(b)=4a,即
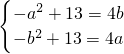
,解得a=1,b=3,
所以[a,b]=[1,3];
③若a<0<b,f(x)在[a,0]上单调递增,在[0,b]上单调递减,
所以f(x)
max=f(0)=13=4b,b=

,f(b)=f(

)=-
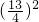
+13>0,
因a<0,最小值4a<0,所以f(x)在x=a是取得最小值4a,即-a
2+13=4a,解得a=-2-

,
此时[a,b]=[-2-

,

],
综上所求区间为[1,3]或[-2-

,

].
分析:(1)先求导数f′(x),由题意可知-2和1是方程f′(x)=0的两根,根据韦达定理列方程组解出即可;
(2)当m=n=0时,f(x)=-x
2+13为二次函数,按区间与对称轴的位置关系分三种情况讨论即可:①若a<b≤0,②若0≤a<b,③若a<0<b,注意检验;
点评:本题考查函数在某点取得极值的条件、二次函数在闭区间上的最值问题,考查分类讨论思想,属中档题.

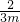 ,-2×1=
,-2×1=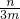 ,解得m=-
,解得m=- ,n=4.
,n=4.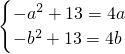 ,
,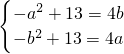 ,解得a=1,b=3,
,解得a=1,b=3, ,f(b)=f(
,f(b)=f( )=-
)=-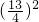 +13>0,
+13>0, ,
, ,
, ],
], ,
, ].
].

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案