
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
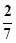 .
.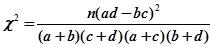 ,其中
,其中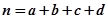 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | 90 | 110 |
| 乙班 | 40 | 60 | 100 |
| 总计 | 60 | 150 | 210 |
 ,可得优秀的人数=
,可得优秀的人数=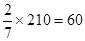 .即可得到乙班优秀的人数,甲班非优秀的人数;(2)假设
.即可得到乙班优秀的人数,甲班非优秀的人数;(2)假设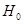 :“成绩与班级无关”.利用公式
:“成绩与班级无关”.利用公式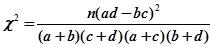 ,计算出
,计算出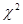 与
与 比较即可得出结论.
比较即可得出结论.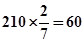 ,又甲班有20人,故乙班有40人.所以2×2列联表如下表所示:
,又甲班有20人,故乙班有40人.所以2×2列联表如下表所示:| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | 90 | 110 |
| 乙班 | 40 | 60 | 100 |
| 总计 | 60 | 150 | 210 |
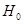 :“成绩与班级无关”.
:“成绩与班级无关”.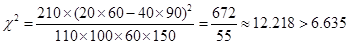
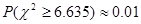 ,因此假设不成立.
,因此假设不成立.

科目:高中数学 来源:不详 题型:解答题
 及天数如下表:
及天数如下表:售出个数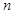 | 10 | 11 | 12 | 13 | 14 | 15 |
| 天数 | 3 | 3 | 3 | 6 | 9 | 6 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
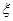 ,求
,求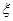 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.ei越小越好 | B.
| ||||||||
C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| ^y=3+2x |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
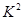 的一个可能取值为( )
的一个可能取值为( )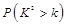 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
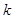 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.期望与方差 | B.独立性检验 | C.正态分布 | D.二项分布列 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
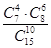 的是( )
的是( )| A.P(ξ=2) | B.P(ξ≤2) |
| C.P(ξ=4) | D.P(ξ≤4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com