(12分)如图,在长方体
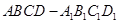
中,
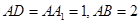
,点E为AB的中点.
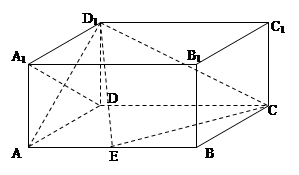
(Ⅰ)求
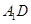
与平面
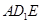
所成的角;
(Ⅱ)求二面角
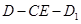
的平面角的正切值.
(Ⅰ)

;(Ⅱ)

.
试题分析:(Ⅰ)在长方体
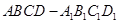
中,求
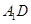
与平面
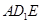
所成的角,关键是找过

点与平面
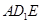
的垂线,注意到
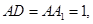
可得

,可猜想

面
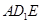
,注意到在长方体
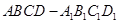
中,

侧面

侧面

,

即
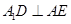
,故

平面
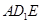
,则得
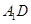
与平面
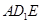
所成的角为

;(Ⅱ)求二面角
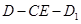
的平面角的正切值,关键是找平面角,注意到

底面

底面

,得

,猜想若

,则

面

,可得

是二面角
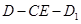
的平面角,事实上在矩形

中,

,且

为

之中点,则

,故可求出二面角
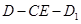
的平面角的正切值.
试题解析:(Ⅰ)在长方体
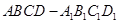
中,

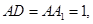

,又在长方体
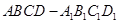
中,

侧面

侧面

,

即
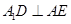
,又

面
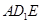
,

面
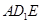
,则
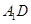
与平面
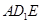
所成的角为

;
(Ⅱ) 连

,在矩形

中,

,且

为

之中点,则

,且

,又

底面

底面

,

,而

面

,

面

面

,则

,所以

是二面角
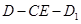
的平面角,在
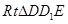
中,

,即二面角
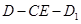
的平面角的正切值为

.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
如图,斜四棱柱

的底面

是矩形,平面

⊥平面

,

分别为
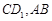
的中点.
求证:
(1)

;(2)

∥平面

.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,在四棱锥

中,底面

为直角梯形,

∥

,

,平面

⊥底面

,

为

的中点,
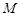
是棱

上的点,

,

,
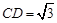
.

(Ⅰ)求证:平面

⊥平面

;
(Ⅱ)若

为棱

的中点,求异面直线

与

所成角的余弦值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,三棱锥

中,

底面

,

,

,

为

的中点,点

在

上,且

.

(Ⅰ)求证:平面

平面

;
(Ⅱ)求平面

与平面

所成的二面角的平面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
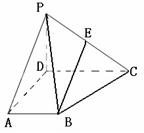
在四棱锥
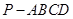
中,侧面
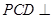
底面
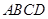
,
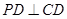
,
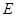
为
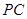
中点,底面
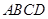
是直角梯形,
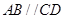
,
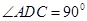
,
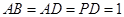
,
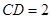
.
(1)求证:
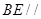
面
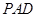
;
(2)求证:面
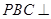
面
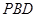
;
(3)设
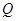
为棱
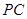
上一点,
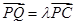
,试确定
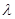
的值使得二面角
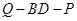
为
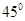
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,在长方体
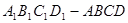
中,
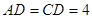
,
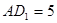
,
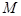
是线段
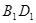
的中点.
(Ⅰ)求证:
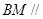
平面

;
(Ⅱ)求直线
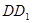
与平面

所成角的正弦值.
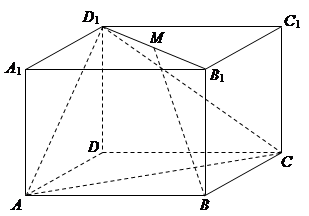
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
如图所示,正方体
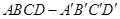
的棱长为1,

分别是棱

,

的中点,过直线

的平面分别与棱

、

交于

,设

,

,给出以下四个命题:
①平面


平面

;
②当且仅当

时,四边形

的面积最小;
③四边形

周长

,

是单调函数;
④四棱锥

的体积

为常函数;
以上命题中真命题的序号为
。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
对于平面
,
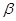
,
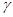
和直线
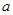
,
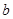
,
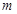
,
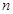
,下列命题中真命题是 ( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
如图,△
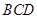
是等边三角形,
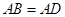
,
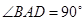
,
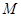
,
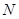
,
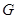
分别是
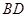
,
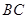
,
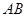
的中点,将△
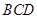
沿
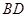
折叠到
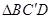
的位置,使得
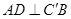
.

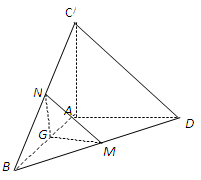
(1)求证:平面
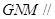
平面
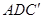
;
(2)求证:
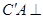
平面
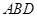
.
查看答案和解析>>

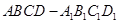 中,
中,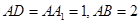 ,点E为AB的中点.
,点E为AB的中点.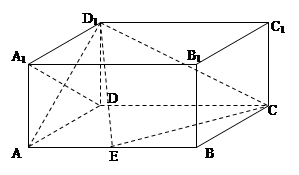
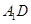 与平面
与平面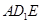 所成的角;
所成的角; 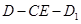 的平面角的正切值.
的平面角的正切值.  中,底面
中,底面 为直角梯形,
为直角梯形, ∥
∥ ,
, ,平面
,平面 ⊥底面
⊥底面 ,
, 为
为 的中点,
的中点,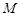 是棱
是棱 上的点,
上的点, ,
, ,
,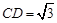 .
.
 ⊥平面
⊥平面 ;
; 为棱
为棱 的中点,求异面直线
的中点,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.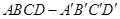 的棱长为1,
的棱长为1,  分别是棱
分别是棱 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题:

 平面
平面 ;
; 时,四边形
时,四边形 的面积最小;
的面积最小;  周长
周长 ,
, 是单调函数;
是单调函数; 的体积
的体积 为常函数;
为常函数;