
分析 (Ⅰ)利用三角函数恒等变换的应用化简函数解析式为f(x)=sin(x+$\frac{π}{4}$)-$\frac{\sqrt{2}}{2}$,利用周期公式即可得解.
(Ⅱ)由已知可求$sin(2A+\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,结合A为锐角,可得$cosA=\frac{{\sqrt{2}}}{2}$,利用余弦定理,基本不等式可求$bc≤\frac{{2+\sqrt{2}}}{2}$,进而利用三角形面积公式即可得解.
解答 (本小题满分12分)
解:(Ⅰ)∵f(x)=$\sqrt{2}$sin$\frac{x}{2}$cos$\frac{x}{2}$-$\sqrt{2}$sin2$\frac{x}{2}$
=$\frac{\sqrt{2}}{2}$sinx-$\sqrt{2}×\frac{1-cosx}{2}$=sin(x+$\frac{π}{4}$)-$\frac{\sqrt{2}}{2}$,…(4分)
∴f(x)的最小正周期为T=$\frac{2π}{1}$=2π;…(5分)
(Ⅱ)由$f(2A)=sin(2A+\frac{π}{4})-\frac{{\sqrt{2}}}{2}=0$,得$sin(2A+\frac{π}{4})=\frac{{\sqrt{2}}}{2}$,
由题意知A为锐角,所以$A=\frac{π}{4}$,可得:$cosA=\frac{{\sqrt{2}}}{2}$,…(8分)
由余弦定理:${a^2}={b^2}+{c^2}-2bccosA可得:1+\sqrt{2}bc={b^2}+{c^2}≥2bc$,
即$bc≤\frac{{2+\sqrt{2}}}{2}$,当且仅当b=c时等号成立,…(10分)
因此$\frac{1}{2}bcsinA≤\frac{{1+\sqrt{2}}}{4}$,
所以△ABC面积的最大值为$\frac{{1+\sqrt{2}}}{4}$.…(12分)
点评 本题主要考查了三角函数恒等变换的应用,周期公式,余弦定理,基本不等式,三角形面积公式在解三角形中的应用,考查了转化思想和运算求解能力,属于中档题.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
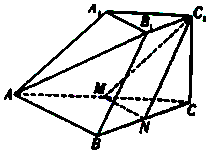 如图,在三棱台ABC-A1B1C1中,CC1⊥平面ABC,AB=2A1B1=2CC1,M,N分别为AC,BC的中点.
如图,在三棱台ABC-A1B1C1中,CC1⊥平面ABC,AB=2A1B1=2CC1,M,N分别为AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图为从空中某个角度俯视北京奥运会主体育场“鸟巢”顶棚所得的局部示意图,在平面直角坐标系中,下列给定的一系列直线中(其中θ为参数,θ∈R),能形成这种效果的只可能是( )
如图为从空中某个角度俯视北京奥运会主体育场“鸟巢”顶棚所得的局部示意图,在平面直角坐标系中,下列给定的一系列直线中(其中θ为参数,θ∈R),能形成这种效果的只可能是( )| A. | y=xsinθ+1 | B. | y=x+cosθ | C. | xcosθ+ysinθ+1=0 | D. | y=xcosθ+sinθ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com