
【题目】设椭圆![]() 的焦点在
的焦点在![]() 轴上.
轴上.
(1)若椭圆![]() 的焦距为1,求椭圆
的焦距为1,求椭圆![]() 的方程;
的方程;
(2)设![]() 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,![]() 为椭圆
为椭圆![]() 上的第一象限内的点,直线
上的第一象限内的点,直线![]() 交
交![]() 轴与点
轴与点![]() ,并且
,并且![]() ,证明:当
,证明:当![]() 变化时,点
变化时,点![]() 在某定直线上.
在某定直线上.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题(1)由椭圆的焦距为![]() ,可得
,可得![]() ,又由
,又由![]() ,从而可以建立关于
,从而可以建立关于![]() 的方程,即可解得
的方程,即可解得![]() ,因此椭圆
,因此椭圆![]() 的方程为
的方程为![]() ;(2)根据题意,可设
;(2)根据题意,可设![]() ,条件中关于
,条件中关于![]() 的约束只有
的约束只有![]() 及
及![]() 在椭圆上,因此需从
在椭圆上,因此需从![]() 即
即![]() 为出发点建立
为出发点建立![]() ,
,![]() 满足的关系式,由题意可得直线
满足的关系式,由题意可得直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
故直线![]() 的方程为
的方程为![]() ,当
,当![]() 时
时![]() ,即点
,即点![]() 的坐标为
的坐标为![]() ,
,
故直线![]() 的斜率为
的斜率为![]() ,因此
,因此![]() ,化简得
,化简得![]() ,又由点
,又由点![]() 在椭圆
在椭圆![]() 上,可得
上,可得![]() ,即点
,即点![]() 在直线
在直线![]() 上.
上.
试题解析:(1)∵焦距为1,∴![]() ,∴
,∴![]() ,
,
故椭圆![]() 的方程为
的方程为![]() ;
;
(2)设![]() ,其中
,其中![]() ,由题设知
,由题设知![]() ,
,
则直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
故直线![]() 的方程为
的方程为![]() ,当
,当![]() 时
时![]() ,即点
,即点![]() 的坐标为
的坐标为![]() ,
,
∴直线![]() 的斜率为
的斜率为![]() ,
,
∵![]() ,∴
,∴![]() ,化简得
,化简得![]()
将上式代入椭圆![]() 的方程,由于
的方程,由于![]() 在第一象限,解得
在第一象限,解得![]() ,即点
,即点![]() 在直线
在直线![]() 上.
上.


科目:高中数学 来源: 题型:
【题目】已知![]() 次多项式
次多项式![]() .如果在一种算法中,计算
.如果在一种算法中,计算![]() 的值共需要
的值共需要![]() 次乘法,计算
次乘法,计算![]() 的值共需要9次运算(6次乘法,3次加法),那么计算
的值共需要9次运算(6次乘法,3次加法),那么计算![]() 的值共需要______次运算.下面给出一种减少运算次数的算法:
的值共需要______次运算.下面给出一种减少运算次数的算法:![]() .利用该算法,计算
.利用该算法,计算![]() 的值共需要6次运算,计算
的值共需要6次运算,计算![]() 的值共需要______次运算;
的值共需要______次运算;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且
的焦点为F,过点F,斜率为1的直线与抛物线C交于点A,B,且![]() .
.
(1)求抛物线C的方程;
(2)过点Q(1,1)作直线交抛物线C于不同于R(1,2)的两点D、E,若直线DR,ER分别交直线![]() 于M,N两点,求|MN|取最小值时直线DE的方程.
于M,N两点,求|MN|取最小值时直线DE的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数对序列![]() 、
、![]() 、
、![]() 、
、![]() ,记
,记![]() ,
,![]() ,其中
,其中![]() 表示
表示![]() 和
和![]() 两个数中最大的数.
两个数中最大的数.
(1)对于数对序列![]() ,
,![]() ,求
,求![]() ,
,![]() 的值;
的值;
(2)记![]() 为
为![]() 、
、![]() 、
、![]() 、
、![]() 四个数中最小值,对于由两个数对
四个数中最小值,对于由两个数对![]() 、
、![]() 组成的数对序列
组成的数对序列![]() 、
、![]() 和
和![]() 、
、![]() ,试分别对
,试分别对![]() 和
和![]() 的两种情况比较
的两种情况比较![]() 和
和![]() 的大小;
的大小;
(3)在由![]() 个数对
个数对![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 组成的所有数对序列中,写出一个数对序列
组成的所有数对序列中,写出一个数对序列![]() 使
使![]() 最小,并写出
最小,并写出![]() 的值.(只需写出结论)
的值.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线![]() 的两顶点为
的两顶点为![]() ,
,![]() ,虚轴两端点为
,虚轴两端点为![]() ,
,![]() ,两焦点为
,两焦点为![]() ,
,![]() ,若以
,若以![]() 为直径的圆内切于菱形
为直径的圆内切于菱形![]() ,切点分别为
,切点分别为![]() ,
,![]() ,
,![]() ,
,![]() .则
.则
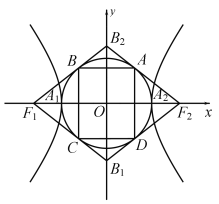
(1)双曲线的离心率![]() ______;
______;
(2)菱形![]() 的面积
的面积![]() 与矩形
与矩形![]() 的面积
的面积![]() 的比值
的比值![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知曲线![]() ,曲线
,曲线![]() ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与![]() 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.
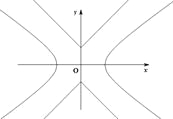
(1)在正确证明![]() 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线![]() 与
与![]() 有公共点,求证
有公共点,求证![]() ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆![]() 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥S-ABCD中,底面ABCD是菱形,![]() ,
,![]() 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
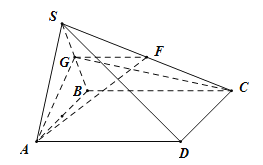
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD,![]() ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小王于2015年底贷款购置了一套房子,根据家庭收入情况,小王选择了10年期每月还款数额相同的还贷方式,且截止2019年底,他没有再购买第二套房子.下图是2016年和2019年小王的家庭收入用于各项支出的比例分配图,根据以上信息,判断下列结论中正确的是( )
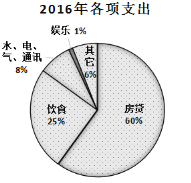
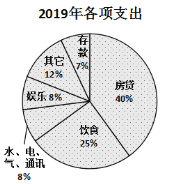
A.小王一家2019年用于饮食的支出费用跟2016年相同
B.小王一家2019年用于其他方面的支出费用是2016年的3倍
C.小王一家2019年的家庭收入比2016年增加了1倍
D.小王一家2019年用于房贷的支出费用比2016年减少了
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com