
【题目】如图所示,将四棱锥S-ABCD的每一个顶点染上一种颜色,并使同一条棱上的两端异色,如果只有5种色可供使用,则不同的染色方法种数为( )

A.240B.360C.420D.960
科目:高中数学 来源: 题型:
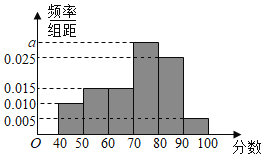
【题目】某校从高二年级学生中随机抽取60名学生,将期中考试的政治成绩(均为整数)分成六段:![]() 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,分别求![]() ,众数,中位数。
,众数,中位数。
(2)估计该校高二年级学生期中考试政治成绩的平均分。
(3)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则在![]() 分数段抽取的人数是多少?
分数段抽取的人数是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凸![]() 边形
边形![]() 玫瑰园的
玫瑰园的![]() 个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
个顶点各栽有1棵红玫瑰,每两棵红玫瑰之间都有一条直小路想通,这些直小路没有出现“三线共点”的情况——它们把花园分割成许多不重叠的区域(三角形、四边形、……),每块区域都栽有一棵白玫瑰(或黑玫瑰).
(1)求出玫瑰园里玫瑰总棵树![]() 的表达式.
的表达式.
(2)花园里能否恰有99棵玫瑰?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个圆周上有9个点,以这9个点为顶点作3个三角形.当这3个三角形无公共顶点且边互不相交时,我们把它称为一种构图.满足这样条件的构图共有( )种.
A. 3 B. 6 C. 9 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
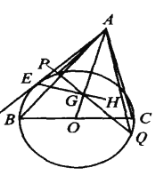
【题目】如图,设H为锐角△ABC的垂心.由顶点A向以BC为直径的⊙O作一条切线AE,切点为E,联结EH交AO于点G,过G任意作⊙O的一条弦PQ.证明:AO 平分∠PAQ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个人独立地破译一个密码,他们能译出密码的概率分别为![]() 和
和![]() .
.
(1)求2个人都译出密码的概率;
(2)求2个人都译不出密码的概率;
(3)求至多1个人都译出密码的概率;
(4)求至少1个人都译出密码的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com