
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到数据如表.预计在今后的销售中,销量与单价仍然服从 (
(  ,
, )的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入-成本),该产品的单价应定为( )元
)的关系,且该产品的成本是4元/件,为使工厂获得最大利润(利润=销售收入-成本),该产品的单价应定为( )元
单价 (元) (元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 (件) (件) | 90 | 84 | 83 | 80 | 75 | 68 |
 B.8 C.
B.8 C.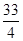 D.
D.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:单选题
设某大学的女生体重 (单位:
(单位: )与身高
)与身高 (单位:
(单位: )具有线性相关关系,根据一组样本数据
)具有线性相关关系,根据一组样本数据 (
(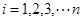 ),用最小二乘法建立的回归方程为
),用最小二乘法建立的回归方程为 ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A. 与 与 具有正的线性相关关系 具有正的线性相关关系 |
B.回归直线过样本点的中心 |
C.若该大学某女生身高增加 ,则其体重约增加 ,则其体重约增加 |
D.若该大学某女生身高为 ,则可断定其体重为 ,则可断定其体重为 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下表提供了某厂节能降耗技术改造后生产某产品过程中记录的产量 (吨)与相应的生产能耗
(吨)与相应的生产能耗 (吨)的几组对应数据. 根据表中提供的数据,求出
(吨)的几组对应数据. 根据表中提供的数据,求出 关于
关于 的线性回归方程是
的线性回归方程是 ,那么表中
,那么表中 的值是( )
的值是( )
 | 3 | 4 | 5 | 6 |
 | 2.5 |  | 4 | 4.5 |
 B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一个容量为20的样本,数据的分组及各组的频数如下:
(10,20 ,2;(20,30
,2;(20,30 ,3;(30,40
,3;(30,40 ,4;(40,50
,4;(40,50 ,5;(50,60
,5;(50,60 ,4;(60,70
,4;(60,70 ,2.
,2.
则样本在区间(10,50 上的频率为( )
上的频率为( )
| A.0.5 | B.0.7 | C.0.25 | D.0.05 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
在独立性检验中,统计量 有两个临界值:3.841和6.635;当
有两个临界值:3.841和6.635;当 >3.841时,有95%的把握说明两个事件有关,当
>3.841时,有95%的把握说明两个事件有关,当 >6.635时,有99%的把握说明两个事件有关,当
>6.635时,有99%的把握说明两个事件有关,当
 3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的
3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的 ="20." 87,根据这一数据分析,认为打鼾与患心脏病之间
="20." 87,根据这一数据分析,认为打鼾与患心脏病之间
| A.有95%的把握认为两者有关 |
| B.约有95%的打鼾者患心脏病 |
| C.有99%的把握认为两者有关 |
| D.约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
下列命题中的真命题是( )
?若命题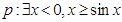 ,命题
,命题 :函数
:函数 仅有两个零点,则命题
仅有两个零点,则命题 为真命题;
为真命题;
?若变量 的一组观测数据
的一组观测数据 均在直线
均在直线 上,则
上,则 的线性相关系数
的线性相关系数 ;
;
?若 ,则使不等式
,则使不等式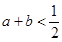 成立的概率是
成立的概率是 .
.
| A.?? | B.?? | C.? | D.?? |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
有一个容量为66的样本,数据的分组及各组的频数如下:
[11.5,15.5) 2 [15.5,19.5) 4 [19.5,23.5) 9
[23.5,27.5) 18 [27.5,31.5) 11 [31.5,35.5) 12
[35.5,39.5) 7 [39.5,43.5) 3
根据样本的概率分布估计,大于或等于31.5的数据约占( )
A.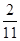 | B.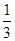 | C.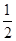 | D.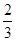 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com