练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】四名同学根据各自的样本数据研究变量之间的相关关系，并求得回归直线方程，分别得到以下四个结论：

    ①与负相关且. ②与负相关且

    ③与正相关且 ④与正相关且

    其中一定不正确的结论的序号是（ ）

    A. ①② B. ②③ C. ③④ D. ①④

    【答案】B

    【解析】根据题意，依次分析4个结论：

    对于①、y与x负相关且=2.756x+7.325，此结论正确，线性回归方程符合负相关的特征；

    对于②、y与x负相关且=3.476x+5.648，此结论误，由线性回归方程知，此两变量的关系是正相关；

    对于③、y与x正相关且=1.226x6.578，此结论误，由线性回归方程知，此两变量的关系是负相关；

    对于④、y与x正相关且=8.967x+8.163，此结论正确，线性回归方程符合正相关的特征；

    故②③一定错误；

    本题选择B选项.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线过点，且方向向量为；在以为极点， 轴的正半轴为极轴的极坐标系中，圆的极坐标方程为.

    （1）求直线的参数方程；

    （2）若直线与圆相交于、两点，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出下列结论：

    ①若扇形的中心角为2，半径为1，则该扇形的面积为1；②函数是偶函数；③点是函数图象的一个对称中心；④函数在上是减函数.其中正确结论的个数为（ ）

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设方程有两个不等的负根， 方程无实根，若“”为真，“”为假，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若函数， ，则对于不同的实数，函数的单调区间个数不可能是（ ）

    A. 1个 B. 2个 C. 3个 D. 5个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知双曲线方程为.

    （1）求该双曲线的实轴长、虚轴长、离心率；

    （2）若抛物线的顶点是该双曲线的中心，而焦点是其左顶点，求抛物线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知一家公司生产某种产品的年固定成本为6万元，每生产1千件需另投入2.9万元，设该公司一年内生产该产品千件并全部销售完，每千件的销售收入为万元，且.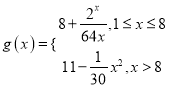

    （1）写出年利润（万元）关于年产量（千件）的函数解析式；

    （2）求该公司生产这一产品的最大年利润及相应的年产量.（年利润=年销售收入-年总成本）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了分析某个高三学生的学习状态，对其下一阶段的学习提供指导性建议．现对他前次考试的数学成绩、物理成绩进行分析．下面是该生次考试的成绩．

    数学

    108

    103

    137

    112

    128

    120

    132

    物理

    74

    71

    88

    76

    84

    81

    86

    （Ⅰ）他的数学成绩与物理成绩哪个更稳定？请给出你的说明；

    （Ⅱ）已知该生的物理成绩与数学成绩是线性相关的，求物理成绩与数学成绩的回归直线方程

    （Ⅲ）若该生的物理成绩达到90分，请你估计他的数学成绩大约是多少？

    （附： ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=log2（2x﹣1）．
    （1）求f（x）的定义域；
    （2）判断函数f（x）的单调性，并用定义证明．

    查看答案和解析>>

    同步练习册答案