
【题目】已知抛物线![]() 过点
过点![]() 则下列结论正确的是( )
则下列结论正确的是( )
A.点P到抛物线焦点的距离为![]()
B.过点P作过抛物线焦点的直线交抛物线于点Q,则△OPQ的面积为![]()
C.过点P与抛物线相切的直线方程为![]()
D.过点P作两条斜率互为相反数的直线交抛物线于M,N点则直线MN的斜率为定值
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=![]() ,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
,PA=AD=2,AB=BC=1,点M、E分别是PA、PD的中点
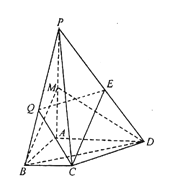
(1)求证:CE//平面BMD
(2)点Q为线段BP中点,求直线PA与平面CEQ所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称,旨在积极发展我国与沿线国家经济合作关系,共同打造政治互信、经济融合、文化包容的命运共同体.自2013年以来,“一带一路”建设成果显著下图是2013-2017年,我国对“一带一路”沿线国家进出口情况统计图,下列描述正确的是( ).
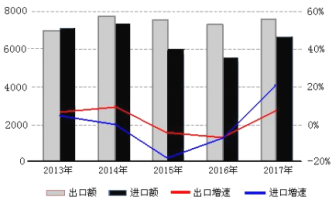
A.这五年,2013年出口额最少
B.这五年,出口总额比进口总额多
C.这五年,出口增速前四年逐年下降
D.这五年,2017年进口增速最快
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国北斗卫星导航系统是中国自行研制的全球卫星导航系统,预计2020年北斗全球系统建设将全面完成.如图是在室外开放的环境下,北斗二代和北斗三代定位模块,分别定位的50个点位的横、纵坐标误差的值,其中“![]() ”表示北斗二代定位模块的误差的值,“+”表示北斗三代定位模块的误差的值.(单位:米)
”表示北斗二代定位模块的误差的值,“+”表示北斗三代定位模块的误差的值.(单位:米)
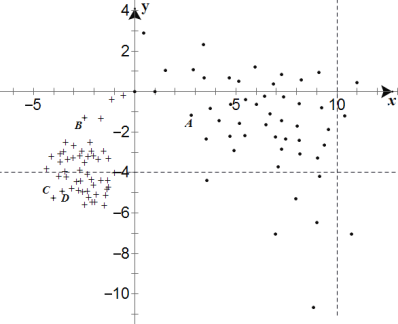
(Ⅰ)从北斗二代定位的50个点位中随机抽取一个,求此点横坐标误差的值大于10米的概率;
(Ⅱ)从图中A,B,C,D四个点位中随机选出两个,记X为其中纵坐标误差的值小于![]() 的点位的个数,求X的分布列和数学期望;
的点位的个数,求X的分布列和数学期望;
(Ⅲ)试比较北斗二代和北斗三代定位模块纵坐标误差的方差的大小.(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,将长方形OAA1O1(及其内部)绕OO1旋转一周形成圆柱,其中![]() ,弧
,弧![]() 的长为
的长为![]() ,AB为⊙O的直径.
,AB为⊙O的直径.
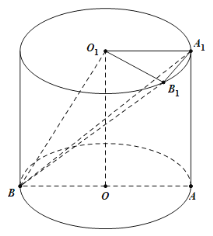
(1)在弧![]() 上是否存在点
上是否存在点![]() (
(![]() ,
,![]() 在平面
在平面![]() 的同侧),使
的同侧),使![]() ,若存在,确定其位置,若不存在,说明理由.
,若存在,确定其位置,若不存在,说明理由.
(2)求二面角![]() 的余弦值
的余弦值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若向量列![]() ,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即
,满足条件:从第二项开始,每一项与它的前一项的差都等于同一个常向量(即坐标都是常数的向量),即![]() (
(![]() ,且
,且![]() ,
,![]() 为常向量),则称这个向量列
为常向量),则称这个向量列![]() 为等差向量列,这个常向量叫做等差向量列的公差,且向量列
为等差向量列,这个常向量叫做等差向量列的公差,且向量列![]() 的前
的前![]() 项和为
项和为![]() .已知等差向量列
.已知等差向量列![]() 满足
满足![]() ,则向量列
,则向量列![]() 的前
的前![]() 项和
项和![]() ( )
( )
A.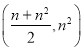 B.
B.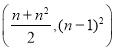
C.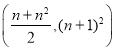 D.
D.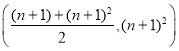
查看答案和解析>>
科目:高中数学 来源: 题型:
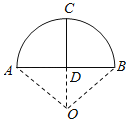
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() (弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为
(弦×矢+矢2),弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差,现有圆心角为![]() ,半径等于
,半径等于![]() 米的弧田,按照上述经验公式计算所得弧田面积约是
米的弧田,按照上述经验公式计算所得弧田面积约是 ![]()
A. ![]() 平方米 B.
平方米 B. ![]() 平方米
平方米
C. ![]() 平方米 D.
平方米 D. ![]() 平方米
平方米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,多边形ABCDEF,四边形ABCD为等腰梯形,![]() ,
,![]() ,
,![]() ,四边形ADEF为直角梯形,
,四边形ADEF为直角梯形,![]() ,
,![]() ,以AD为折痕把等腰梯形ABCD折起,使得平面
,以AD为折痕把等腰梯形ABCD折起,使得平面![]() 平面ADEF,如图2.
平面ADEF,如图2.
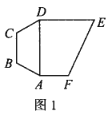
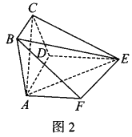
(Ⅰ)证明:![]() 平面CDE;
平面CDE;
(Ⅱ)求直线BE与平面EAC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com