
ΓΨΧβΡΩΓΩ”…÷–―κΒγ ”Χ®ΉέΚœΤΒΒά![]() ΚΆΈ®÷Ύ¥ΪΟΫΝΣΚœ÷ΤΉςΒΡ
ΚΆΈ®÷Ύ¥ΪΟΫΝΣΚœ÷ΤΉςΒΡ![]() ΩΣΫ≤ά≤
ΩΣΫ≤ά≤![]() «÷–Ιζ ΉΒΒ«ύΡξΒγ ”ΙΪΩΣΩΈΘ§ΟΩΤΎΫΎΡΩ”…“ΜΈΜ÷ΣΟϊ»Υ ΩΫ≤ ωΉ‘ΦΚΒΡΙ ¬Θ§Ζ÷œμΥϊΟ«Ε‘”Ύ…ζΜνΚΆ…ζΟϋΒΡΗ–ΈρΘ§Ηχ”η÷–Ιζ«ύΡξœ÷ ΒΒΡΧ÷¬έΚΆ–ΡΝιΒΡΉΧ―χΘ§Χ÷¬έ«ύΡξΟ«ΒΡ»Υ…ζΈ ΧβΘ§Ά§ ±“≤‘ΎΧ÷¬έ«ύ¥Κ÷–ΙζΒΡ…γΜαΈ ΧβΘ§ ήΒΫ«ύΡξΙέ÷ΎΒΡœ≤Α°Θ§ΈΣΝΥΝΥΫβΙέ÷ΎΕ‘ΫΎΡΩΒΡœ≤Α°≥ΧΕ»Θ§Βγ ”Χ®ΥφΜζΒς≤ιΝΥAΓΔBΝΫΗωΒΊ«χΒΡ100ΟϊΙέ÷ΎΘ§ΒΟΒΫ»γ±μΒΡ
«÷–Ιζ ΉΒΒ«ύΡξΒγ ”ΙΪΩΣΩΈΘ§ΟΩΤΎΫΎΡΩ”…“ΜΈΜ÷ΣΟϊ»Υ ΩΫ≤ ωΉ‘ΦΚΒΡΙ ¬Θ§Ζ÷œμΥϊΟ«Ε‘”Ύ…ζΜνΚΆ…ζΟϋΒΡΗ–ΈρΘ§Ηχ”η÷–Ιζ«ύΡξœ÷ ΒΒΡΧ÷¬έΚΆ–ΡΝιΒΡΉΧ―χΘ§Χ÷¬έ«ύΡξΟ«ΒΡ»Υ…ζΈ ΧβΘ§Ά§ ±“≤‘ΎΧ÷¬έ«ύ¥Κ÷–ΙζΒΡ…γΜαΈ ΧβΘ§ ήΒΫ«ύΡξΙέ÷ΎΒΡœ≤Α°Θ§ΈΣΝΥΝΥΫβΙέ÷ΎΕ‘ΫΎΡΩΒΡœ≤Α°≥ΧΕ»Θ§Βγ ”Χ®ΥφΜζΒς≤ιΝΥAΓΔBΝΫΗωΒΊ«χΒΡ100ΟϊΙέ÷ΎΘ§ΒΟΒΫ»γ±μΒΡ![]() Ν–ΝΣ±μΘ§“―÷Σ‘Ύ±ΜΒς≤ιΒΡ100ΟϊΙέ÷Ύ÷–ΥφΜζ≥ι»Γ1ΟϊΘ§ΗΟΙέ÷Ύ «BΒΊ«χΒ±÷–ΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΙέ÷ΎΒΡΗ≈¬ ΈΣ
Ν–ΝΣ±μΘ§“―÷Σ‘Ύ±ΜΒς≤ιΒΡ100ΟϊΙέ÷Ύ÷–ΥφΜζ≥ι»Γ1ΟϊΘ§ΗΟΙέ÷Ύ «BΒΊ«χΒ±÷–ΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΙέ÷ΎΒΡΗ≈¬ ΈΣ![]() Θ°
Θ°
Ζ«≥Θ¬ζ“β | ¬ζ“β | ΚœΦΤ | |
A | 30 | 15 | |
B | |||
ΚœΦΤ |
![]() Άξ≥……œ ω±μΗώ≤ΔΗυΨί±μΗώ≈–Εœ «Ζώ”–
Άξ≥……œ ω±μΗώ≤ΔΗυΨί±μΗώ≈–Εœ «Ζώ”–![]() ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘΜ
ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘΜ
![]() »τ“‘≥ι―υΒς≤ιΒΡΤΒ¬ ΈΣΗ≈¬ Θ§¥”AΒΊ«χΥφΜζ≥ι»Γ3»ΥΘ§…η≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡ»Υ ΐΈΣXΘ§«σXΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘ°
»τ“‘≥ι―υΒς≤ιΒΡΤΒ¬ ΈΣΗ≈¬ Θ§¥”AΒΊ«χΥφΜζ≥ι»Γ3»ΥΘ§…η≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡ»Υ ΐΈΣXΘ§«σXΒΡΖ÷≤ΦΝ–ΚΆΤΎΆϊΘ°
|
|
|
|
|
|
|
|
ΗΫΘΚ≤ΈΩΦΙΪ ΫΘΚ![]() Θ°
Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©ΟΜ”–![]() ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘ°Θ®2Θ©ΦϊΫβΈωΘ§ΤΎΆϊΈΣ2
ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘ°Θ®2Θ©ΦϊΫβΈωΘ§ΤΎΆϊΈΣ2
ΓΨΫβΈωΓΩ
Θ®1Θ©Άξ≥…![]() Ν–ΝΣ±μΘ§«σ≥ω
Ν–ΝΣ±μΘ§«σ≥ω![]() Θ§¥”ΕχΟΜ”–
Θ§¥”ΕχΟΜ”–![]() ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘ°
ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘ°
Θ®2Θ©¥”![]() ΒΊ«χΥφΜζ≥ι»Γ
ΒΊ«χΥφΜζ≥ι»Γ![]() »ΥΘ§≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΗ≈¬ ΈΣ
»ΥΘ§≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΗ≈¬ ΈΣ![]() Θ§ΥφΜζ≥ι»Γ
Θ§ΥφΜζ≥ι»Γ![]() »ΥΘ§
»ΥΘ§![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ
ΒΡΩ…Ρή»Γ÷ΒΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§”…¥ΥΡή«σ≥ω
Θ§”…¥ΥΡή«σ≥ω![]() ΒΡΖ÷≤ΦΝ–ΚΆ
ΒΡΖ÷≤ΦΝ–ΚΆ![]() .
.
Θ®1Θ©Άξ≥…![]() Ν–ΝΣ±μ»γœ¬ΘΚ
Ν–ΝΣ±μ»γœ¬ΘΚ
Ζ«≥Θ¬ζ“β | ¬ζ“β | ΚœΦΤ | |
A | 30 | 15 | 45 |
B | 35 | 20 | 55 |
ΚœΦΤ | 65 | 35 | 100 |
‘ρ![]() Θ§
Θ§
![]() ΟΜ”–
ΟΜ”–![]() ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘ°
ΒΡΑ―Έ’»œΈΣΙέ÷ΎΒΡ¬ζ“β≥ΧΕ»”κΥυ‘ΎΒΊ«χ”–ΙΊœΒΘ°
Θ®2Θ©¥”![]() ΒΊ«χΥφΜζ≥ι»Γ1»ΥΘ§≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΗ≈¬ ΈΣ
ΒΊ«χΥφΜζ≥ι»Γ1»ΥΘ§≥ιΒΫΒΡΙέ÷ΎΓΑΖ«≥Θ¬ζ“βΓ±ΒΡΗ≈¬ ΈΣ![]() Θ§
Θ§
ΥφΜζ≥ι»Γ![]() »ΥΘ§
»ΥΘ§![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ
ΒΡΩ…Ρή»Γ÷ΒΈΣ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
![]() Θ°
Θ°


 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§![]() .
.
Θ®1Θ©Β±![]() ±Θ§«σΚ· ΐ
±Θ§«σΚ· ΐ![]() ΒΡΒΞΒς«χΦδΦΑΦΪ÷ΒΘΜ
ΒΡΒΞΒς«χΦδΦΑΦΪ÷ΒΘΜ
Θ®2Θ©Χ÷¬έΚ· ΐ![]() ΒΡΝψΒψΗω ΐ.
ΒΡΝψΒψΗω ΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΙΐΒψ
ΙΐΒψ![]() Θ§«“PΒΫ≈ΉΈοœΏΫΙΒψΒΡΨύάκΈΣ2÷±œΏ
Θ§«“PΒΫ≈ΉΈοœΏΫΙΒψΒΡΨύάκΈΣ2÷±œΏ![]() ΙΐΒψ
ΙΐΒψ![]() Θ§«“”κ≈ΉΈοœΏœύΫΜ”ΎAΘ§BΝΫΒψ.
Θ§«“”κ≈ΉΈοœΏœύΫΜ”ΎAΘ§BΝΫΒψ.
Θ®ΔώΘ©«σ≈ΉΈοœΏΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τΒψQ«ΓΈΣœΏΕΈABΒΡ÷–ΒψΘ§«σ÷±œΏ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®ΔσΘ©ΙΐΒψ![]() Ής÷±œΏMAΘ§MBΖ÷±πΫΜ≈ΉΈοœΏ”ΎCΘ§DΝΫΒψΘ§«κΈ CΘ§DΘ§Q»ΐΒψΡήΖώΙ≤œΏΘΩ»τΡήΘ§«σ≥ω÷±œΏ
Ής÷±œΏMAΘ§MBΖ÷±πΫΜ≈ΉΈοœΏ”ΎCΘ§DΝΫΒψΘ§«κΈ CΘ§DΘ§Q»ΐΒψΡήΖώΙ≤œΏΘΩ»τΡήΘ§«σ≥ω÷±œΏ![]() ΒΡ–±¬
ΒΡ–±¬ ![]() ΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”….
ΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§‘ρœ¬ ωΫα¬έ÷–¥μΈσΒΡ «Θ® Θ©
Θ§‘ρœ¬ ωΫα¬έ÷–¥μΈσΒΡ «Θ® Θ©
A.»τ![]() ‘Ύ
‘Ύ![]() ”–«“Ϋω”–
”–«“Ϋω”–![]() ΗωΝψΒψΘ§‘ρ
ΗωΝψΒψΘ§‘ρ![]() ‘Ύ
‘Ύ![]() ”–«“Ϋω”–
”–«“Ϋω”–![]() ΗωΦΪ–Γ÷ΒΒψ
ΗωΦΪ–Γ÷ΒΒψ
B.»τ![]() ‘Ύ
‘Ύ![]() ”–«“Ϋω”–
”–«“Ϋω”–![]() ΗωΝψΒψΘ§‘ρ
ΗωΝψΒψΘ§‘ρ![]() ‘Ύ
‘Ύ![]() …œΒΞΒςΒί‘ω
…œΒΞΒςΒί‘ω
C.»τ![]() ‘Ύ
‘Ύ![]() ”–«“Ϋω”–
”–«“Ϋω”–![]() ΗωΝψΒψΘ§‘ρ
ΗωΝψΒψΘ§‘ρ![]() ΒΡΖΕΈß «
ΒΡΖΕΈß «![]()
D.»τ![]() ΆΦœώΙΊ”Ύ
ΆΦœώΙΊ”Ύ![]() Ε‘≥ΤΘ§«“‘Ύ
Ε‘≥ΤΘ§«“‘Ύ![]() ΒΞΒςΘ§‘ρ
ΒΞΒςΘ§‘ρ![]() ΒΡΉν¥σ÷ΒΈΣ
ΒΡΉν¥σ÷ΒΈΣ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫ––ΝυΟφΧεABCD©¹A1B1C1D1÷–Θ§AA1ΘΫA1DΘ§ABΘΫBCΘ§ΓœABCΘΫ120Γψ.
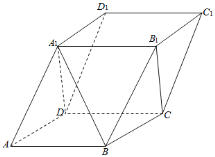
Θ®1Θ©÷ΛΟςΘΚADΓΆBA1ΘΜ
Θ®2Θ©»τΤΫΟφADD1A1ΓΆΤΫΟφABCDΘ§«“A1DΘΫABΘ§«σ÷±œΏBA1”κΤΫΟφA1B1CDΥυ≥…Ϋ«ΒΡ’ΐœ“÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΆ÷‘≤![]() ΫΙΒψ‘Ύ
ΫΙΒψ‘Ύ![]() ÷α…œΘ§άκ–Ρ¬ ΈΣ
÷α…œΘ§άκ–Ρ¬ ΈΣ![]() Θ§…œΫΙΒψΒΫ…œΕΞΒψΨύάκΈΣ
Θ§…œΫΙΒψΒΫ…œΕΞΒψΨύάκΈΣ![]() .
.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡ±ξΉΦΖΫ≥ΧΘΜ
ΒΡ±ξΉΦΖΫ≥ΧΘΜ
Θ®2Θ©÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ΫΜ”κ
ΫΜ”κ![]() ΝΫΒψΘ§
ΝΫΒψΘ§![]() ΈΣΉχ±ξ‘≠ΒψΘ§
ΈΣΉχ±ξ‘≠ΒψΘ§![]() ΒΡΟφΜΐ
ΒΡΟφΜΐ![]() Θ§‘ρ
Θ§‘ρ![]() «ΖώΈΣΕ®÷ΒΘ§»τ ««σ≥ωΕ®÷ΒΘΜ»τ≤Μ «Θ§ΥΒΟςάμ”….
«ΖώΈΣΕ®÷ΒΘ§»τ ««σ≥ωΕ®÷ΒΘΜ»τ≤Μ «Θ§ΥΒΟςάμ”….
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ![]() «Ε®“ε‘Ύ
«Ε®“ε‘Ύ![]() …œΒΡΚ· ΐΘ§¬ζΉψ
…œΒΡΚ· ΐΘ§¬ζΉψ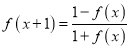 .
.
Θ®1Θ©÷ΛΟςΘΚ2 «Κ· ΐ![]() ΒΡ÷ήΤΎΘΜ
ΒΡ÷ήΤΎΘΜ
Θ®2Θ©Β±![]() ±Θ§
±Θ§![]() Θ§«σ
Θ§«σ![]() ‘Ύ
‘Ύ![]() ±ΒΡΫβΈω ΫΘ§≤Δ–¥≥ω
±ΒΡΫβΈω ΫΘ§≤Δ–¥≥ω![]() ‘Ύ
‘Ύ![]() Θ®
Θ®![]() Θ© ±ΒΡΫβΈω ΫΘΜ
Θ© ±ΒΡΫβΈω ΫΘΜ
Θ®3Θ©Ε‘”ΎΘ®2Θ©÷–ΒΡΚ· ΐ![]() Θ§»τΙΊ”ΎxΒΡΖΫ≥Χ
Θ§»τΙΊ”ΎxΒΡΖΫ≥Χ![]() «ΓΚΟ”–20ΗωΫβΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈß.
«ΓΚΟ”–20ΗωΫβΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐ![]() Θ®a>0«“aΓΌ1Θ© «ΤφΚ· ΐΘ°
Θ®a>0«“aΓΌ1Θ© «ΤφΚ· ΐΘ°
Θ®1Θ©«σ≥Θ ΐkΒΡ÷ΒΘΜ
Θ®2Θ©»τ“―÷ΣfΘ®1Θ©=![]() Θ§«“Κ· ΐ
Θ§«“Κ· ΐ![]() ‘Ύ«χΦδ[1Θ§+Γό]Θ©…œΒΡΉν–Γ÷ΒΈΣΓΣ2Θ§«σ Β ΐmΒΡ÷ΒΘ°
‘Ύ«χΦδ[1Θ§+Γό]Θ©…œΒΡΉν–Γ÷ΒΈΣΓΣ2Θ§«σ Β ΐmΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() Θ§‘Ύx÷α’ΐΑκ÷α…œ»Έ“β―ΓΕ®“ΜΒψ
Θ§‘Ύx÷α’ΐΑκ÷α…œ»Έ“β―ΓΕ®“ΜΒψ![]()
![]() Θ§ΙΐΒψMΉς”κx÷α¥Ι÷±ΒΡ÷±œΏΫΜC”ΎPΘ§OΝΫΒψ.
Θ§ΙΐΒψMΉς”κx÷α¥Ι÷±ΒΡ÷±œΏΫΜC”ΎPΘ§OΝΫΒψ.
Θ®1Θ©…η![]() Θ§÷ΛΟςΘΚ≈ΉΈοœΏ
Θ§÷ΛΟςΘΚ≈ΉΈοœΏ![]() ‘ΎΒψPΘ§Q¥ΠΒΡ«–œΏΖΫ≥ΧΒΡΫΜΒψN”κΒψMΙΊ”Ύ‘≠ΒψOΕ‘≥ΤΘΜ
‘ΎΒψPΘ§Q¥ΠΒΡ«–œΏΖΫ≥ΧΒΡΫΜΒψN”κΒψMΙΊ”Ύ‘≠ΒψOΕ‘≥ΤΘΜ
Θ®2Θ©Ά®ΙΐΫβ¥πΘ®1Θ©Θ§≤¬œκ«σΙΐ≈ΉΈοœΏ![]()
![]() …œ“ΜΒψ
…œ“ΜΒψ![]() Θ®≤ΜΈΣ‘≠ΒψΘ©ΒΡ«–œΏΖΫ≥ΧΒΡ“Μ÷÷ΉωΖ®Θ§≤ΔΦ”“‘÷ΛΟς.
Θ®≤ΜΈΣ‘≠ΒψΘ©ΒΡ«–œΏΖΫ≥ΧΒΡ“Μ÷÷ΉωΖ®Θ§≤ΔΦ”“‘÷ΛΟς.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com