
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,且
,且![]() 时
时![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,对任意
,对任意![]() ,都有
,都有![]() .
.
(1)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(2)令![]() 若对任意的
若对任意的![]() ,不等式
,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,在正四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,下列四个结论不成立的是 ( )
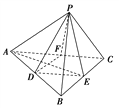
A. BC∥平面PDF B. DF⊥平面PAE
C. 平面PDF⊥平面PAE D. 平面PDE⊥平面ABC
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下给出五个命题,其中真命题的序号为______
①函数![]() 在区间
在区间![]() 上存在一个零点,则
上存在一个零点,则![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
②“任意菱形的对角线一定相等”的否定是“菱形的对角线一定不相等”;
③![]() ,
,![]() ;
;
④若![]() ,则
,则![]() ;
;
⑤“![]() ”是“
”是“![]() 成等比数列”的充分不必要条件.
成等比数列”的充分不必要条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线![]() 的焦点作直线交抛物线于
的焦点作直线交抛物线于![]() ,
,![]() 两点,若
两点,若![]() ,则
,则![]() 的值为( )
的值为( )
A. 10 B. 8 C. 6 D. 4
【答案】B
【解析】
根据过抛物线焦点的弦长公式,利用题目所给已知条件,求得弦长![]() .
.
根据过抛物线焦点的弦长公式有![]() .故选B.
.故选B.
【点睛】
本小题主要考查过抛物线焦点的弦长公式,即![]() .要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
.要注意只有过抛物线焦点的弦长才可以使用.属于基础题.
【题型】单选题
【结束】
10
【题目】已知椭圆![]() :
: ![]() 的右顶点、上顶点分别为
的右顶点、上顶点分别为![]() 、
、![]() ,坐标原点到直线
,坐标原点到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,则椭圆
,则椭圆![]() 的方程为( )
的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点为![]() ,
,![]() 且离心率
且离心率![]() .
.
(1)求双曲线的方程;
(2)求以点![]() 为中点的弦所在的直线方程.
为中点的弦所在的直线方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据焦点坐标求得![]() ,根据离心率及
,根据离心率及![]() 求得
求得![]() 的值,进而求得双曲线的标准方程.(2)设出
的值,进而求得双曲线的标准方程.(2)设出![]() 两点的坐标,利用点差法求得弦所在直线的斜率,再由点斜式求得弦所在的直线方程.
两点的坐标,利用点差法求得弦所在直线的斜率,再由点斜式求得弦所在的直线方程.
(1) 由题可得![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
所以双曲线方程 ![]() .
.
(2)设弦的两端点分别为![]() ,
,![]() ,
,
则由点差法有: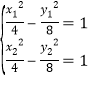 , 上下式相减有:
, 上下式相减有:![]()
又因为![]() 为中点,所以
为中点,所以![]() ,
,![]() ,
,
∴![]() ,所以由直线的点斜式可得
,所以由直线的点斜式可得![]() ,
,
即直线的方程为![]() .
.
经检验满足题意.
【点睛】
本小题主要考查双曲线标准方程的求法,考查利用点差法求解有关弦的中点有关的问题,属于中档题
【题型】解答题
【结束】
19
【题目】某投资公司计划投资![]() ,
,![]() 两种金融产品,根据市场调查与预测,
两种金融产品,根据市场调查与预测,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() ,
,![]() 产品的利润
产品的利润![]() 与投资金额
与投资金额![]() 的函数关系为
的函数关系为![]() .(注:利润与投资金额单位:万元)
.(注:利润与投资金额单位:万元)
(1)该公司已有100万元资金,并全部投入![]() ,
,![]() 两种产品中,其中
两种产品中,其中![]() 万元资金投入
万元资金投入![]() 产品,试把
产品,试把![]() ,
,![]() 两种产品利润总和表示为
两种产品利润总和表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)试问:怎样分配这100万元资金,才能使公司获得最大利润?其最大利润为多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内动点![]() 到两定点
到两定点![]() 和
和![]() 的距离之和为4.
的距离之和为4.
(Ⅰ)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)已知直线![]() 和
和![]() 的倾斜角均为
的倾斜角均为![]() ,直线
,直线![]() 过坐标原点
过坐标原点![]() 且与曲线
且与曲线![]() 相交于
相交于![]() ,
, ![]() 两点,直线
两点,直线![]() 过点
过点![]() 且与曲线
且与曲线![]() 是交于
是交于![]() ,
, ![]() 两点,求证:对任意
两点,求证:对任意![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com