
【题目】已知数列![]() 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.设数列![]() 的前n项和为
的前n项和为![]() 且满足
且满足![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() 求正整数
求正整数![]() 的值;
的值;
(3)是否存在正整数![]() ,使得
,使得![]() 恰好为数列
恰好为数列![]() 的一项?若存在,求出所有满足条件的正整数
的一项?若存在,求出所有满足条件的正整数![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
【答案】(1)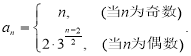 (2)
(2)![]() (3)存在两个正整数
(3)存在两个正整数![]() ;
;![]() 1或2
1或2
【解析】
(1)设![]() 的奇数项构成的等差数列的公差为
的奇数项构成的等差数列的公差为![]() ,偶数项构成的等比数列的公比为
,偶数项构成的等比数列的公比为![]() ,运用通项公式,解方程可得
,运用通项公式,解方程可得![]() ,
,![]() ,即可得到所求通项公式;(2)当
,即可得到所求通项公式;(2)当![]() 为奇数时,当
为奇数时,当![]() 为偶数时,运用通项公式,解方程可得
为偶数时,运用通项公式,解方程可得![]() 的值;(3)求得
的值;(3)求得![]() ,
,![]() ,若
,若![]() 为数列
为数列![]() 中的一项,整理化简求得
中的一项,整理化简求得![]() ,
,![]() 的值,再由数学归纳法证明,即可得到结论.
的值,再由数学归纳法证明,即可得到结论.
(1)设![]() 的奇数项构成的等差数列的公差为
的奇数项构成的等差数列的公差为![]() 偶数项构成的等比数列的公比为
偶数项构成的等比数列的公比为![]() 则
则![]()
由已知,得![]()
故数列![]() 的通项公式为:
的通项公式为: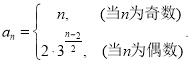
(2)当k为奇数时,由![]() 得
得![]()
由于![]() 而
而![]() 仅在
仅在![]() 时为正整数,与
时为正整数,与![]() 为奇数矛盾!
为奇数矛盾!
当k为偶数时,由![]() 得
得![]()
综上,得![]()
(3)由(1)可求得![]()
![]()
若![]() 为数列
为数列![]() 中的一项,则
中的一项,则![]() (
(![]() 为正奇数)或
为正奇数)或![]() (
(![]() 为正偶数)
为正偶数)
(i)若![]() (
(![]() 为正奇数),则
为正奇数),则![]()
当![]() 时,
时,![]() ,结论成立;
,结论成立;
当![]() 时,
时,![]() 由
由![]() 得
得![]() 解得
解得![]()
由于![]() 为正奇数,故此时满足条件的正整数k不存在.
为正奇数,故此时满足条件的正整数k不存在.
(ii)若![]() (
(![]() 为正偶数),
为正偶数),
显然![]() ,则
,则
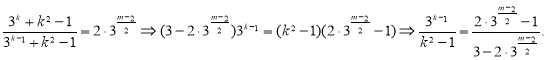
由![]() 得
得![]() 得
得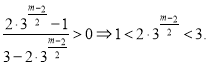
由![]() 为正偶数得
为正偶数得![]() 为正偶数,因此
为正偶数,因此![]() ,从而
,从而![]()
当![]() 时,
时,![]() ;下面用数学归纳法证明:当
;下面用数学归纳法证明:当![]() 时,
时,![]()
①当![]() 时,显然
时,显然![]() ;
;
②假设当![]() 时,有
时,有![]() ;则当
;则当![]() 时,
时,
由![]() 得
得![]() ,
,
故![]()
即![]() 时,结论成立.
时,结论成立.
由①,②知:![]() 时,
时,![]()
综合(i),(ii)得:存在两个正整数![]() ,
,![]() 1或2,使
1或2,使![]() 为数列
为数列![]() 中的项.
中的项.


科目:高中数学 来源: 题型:
【题目】甲、乙两名射击运动员在进行射击训练,已知甲命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,乙命中10环,9环,8环的概率分别是
,乙命中10环,9环,8环的概率分别是![]() ,
,![]() ,
,![]() ,任意两次射击相互独立.
,任意两次射击相互独立.
(1)求甲运动员两次射击命中环数之和恰好为18的概率;
(2)现在甲、乙两人进行射击比赛,每一轮比赛两人各射击1次,环数高于对方为胜,环数低于对方为负,环数相等为平局,规定连续胜利两轮的选手为最终的胜者,比赛结束,求恰好进行3轮射击后比赛结束的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 与
与![]() 满足
满足![]() ,
,![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且数列
,且数列![]() 是公比等于2的等比数列,求
是公比等于2的等比数列,求![]() 的值,使数列
的值,使数列![]() 也是等比数列;
也是等比数列;
(3)若![]() ,且
,且![]() ,数列
,数列![]() 有最大值
有最大值![]() 与最小值
与最小值![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B是海岸线OM、ON上两个码头,海中小岛有码头Q到海岸线OM、ON的距离分别为![]() 、
、![]() ,测得
,测得![]() ,
,![]() ,以点O为坐标原点,射线OM为x轴的正半轴,建立如图所示的直角坐标系,一艘游轮以
,以点O为坐标原点,射线OM为x轴的正半轴,建立如图所示的直角坐标系,一艘游轮以![]() 小时的平均速度在水上旅游线AB航行(将航线AB看作直线,码头Q在第一象限,航线BB经过点Q).
小时的平均速度在水上旅游线AB航行(将航线AB看作直线,码头Q在第一象限,航线BB经过点Q).
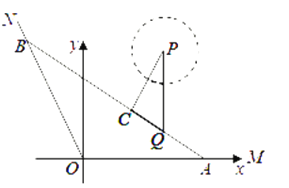
(1)问游轮自码头A沿![]() 方向开往码头B共需多少分钟?
方向开往码头B共需多少分钟?
(2)海中有一处景点P(设点P在![]() 平面内,
平面内,![]() ,且
,且![]() ),游轮无法靠近,求游轮在水上旅游线AB航行时离景点P最近的点C的坐标.
),游轮无法靠近,求游轮在水上旅游线AB航行时离景点P最近的点C的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于双曲线![]() :
:![]() (
(![]() ),若点
),若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的外部;若点
的外部;若点![]() 满足
满足![]() ,则称
,则称![]() 在
在![]() 的内部.
的内部.
(1)若直线![]() 上点都在
上点都在![]() 的外部,求
的外部,求![]() 的取值范围;
的取值范围;
(2)若![]() 过点
过点![]() ,圆
,圆![]() (
(![]() )在
)在![]() 内部及
内部及![]() 上的点构成的圆弧长等于该圆周长的一半,求
上的点构成的圆弧长等于该圆周长的一半,求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的取值范围;
的取值范围;
(3)若曲线![]() (
(![]() )上的点都在
)上的点都在![]() 的外部,求
的外部,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+(x-1)|x-a|.
(1)若a=-1,解方程f(x)=1;
(2)若函数f(x)在R上单调递增,求实数a的取值范围;
(3)是否存在实数a,使不等式f(x)≥2x-3对任意x∈R恒成立?若存在,求出a的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 由方程到
由方程到![]() 确定,对于函数
确定,对于函数![]() 给出下列命题:
给出下列命题:
①对任意![]()
![]() ,都有
,都有![]() 恒成立:
恒成立:
②![]()
![]() ,使得
,使得![]() 且
且![]() 同时成立;
同时成立;
③对于任意![]()
![]() 恒成立;
恒成立;
④对任意,![]()
![]()
![]() ,
,
都有![]() 恒成立.其中正确的命题共有( )
恒成立.其中正确的命题共有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com