
【题目】如图所示,在直角梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 底面
底面![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】已知圆C1的参数方程为![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,圆C2的极坐标方程为![]() .
.
(1)将圆C1的参数方程化为普通方程,将圆C2的极坐标方程化为直角坐标方程;
(2)圆C1、C2是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-5 不等式选讲
已知函数f(x)=|x-1|-2|x+1|的最大值为m.
(1)求m;
(2)若a,b,c∈(0,+∞),a2+2b2+c2=2m,求ab+bc的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对定义域D内的每一个x1,都存在唯一的x2∈D,使得
对定义域D内的每一个x1,都存在唯一的x2∈D,使得![]() 成立,则称f (x)为“自倒函数”.给出下列命题:
成立,则称f (x)为“自倒函数”.给出下列命题:
①![]() 是自倒函数;
是自倒函数;
②自倒函数f (x)可以是奇函数;
③自倒函数f (x)的值域可以是R;
④若![]() 都是自倒函数,且定义域相同,则
都是自倒函数,且定义域相同,则![]() 也是自倒函数.
也是自倒函数.
则以上命题正确的是_______(写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·辽宁五校联考)某车间加工零件的数量x与加工时间y的统计数据如表:
零件数x(个) | 10 | 20 | 30 |
加工时间y(分钟) | 21 | 30 | 39 |
现已求得上表数据的线性回归方程![]() =
=![]() +
+![]() 中的
中的![]() 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A. 84分钟 B. 94分钟
C. 102分钟 D. 112分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2017·成都高中毕业第一次诊断)已知双曲线![]() (a>0,b>0)的左、右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
(a>0,b>0)的左、右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 3
D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】博鳌亚洲论坛2015年会员大会于3月27日在海南博鳌举办,大会组织者对招募的100名服务志愿者培训后,组织一次![]() 知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.
知识竞赛,将所得成绩制成如右频率分布直方图(假定每个分数段内的成绩均匀分布),组织者计划对成绩前20名的参赛者进行奖励.
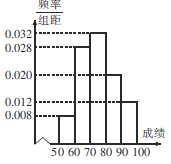
(1)试确定受奖励的分数线;
(2)从受奖励的20人中利用分层抽样抽取5人,再从抽取的5人中抽取2人在主会场服务,试求2人成绩都在90分以上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com