
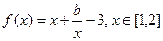
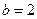 时,求
时,求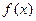 的值域;
的值域;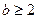 时,
时,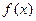 的最大值为M,最小值为m,且满足:
的最大值为M,最小值为m,且满足: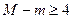 ,求b的取值范围.
,求b的取值范围. 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源:不详 题型:单选题
 与时间
与时间 (月)的关系:
(月)的关系: ,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过
,有以下叙述:① 这个指数函数的底数是2;②第5个月的浮萍的面积就会超过 ;③浮萍从
;③浮萍从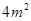 蔓延到
蔓延到 需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到
需要经过1.5个月;④浮萍每个月增加的面积都相等;⑤若浮萍蔓延到 、
、 、
、 所经过的时间分别为
所经过的时间分别为 ,则
,则 .其中正确的是( )
.其中正确的是( )
| A.①② | B.①②⑤ | C.①②③④ | D.②③④⑤ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为
厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为 元(
元( 为常数,且
为常数,且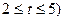 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元( ),根据市场调查,销售量
),根据市场调查,销售量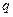 与
与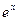 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.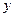 元与每公斤蘑菇的出厂价
元与每公斤蘑菇的出厂价 元的函数关系式;
元的函数关系式; ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 为多少元时,该工厂的利润
为多少元时,该工厂的利润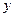 最大,并求最大值.
最大,并求最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 时间 | 第4天 | 第32天 | 第60天 | 第90天 |
| 价格(千元) | 23 | 30 | 22 | 7 |
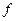 (
( )关于时间
)关于时间 的函数表达式(
的函数表达式( 表示投入市场的第
表示投入市场的第 天);
天); (
( )与时间
)与时间 的函数关系是
的函数关系是 ,求日销售额的最大值,并求第几天销售额最高?
,求日销售额的最大值,并求第几天销售额最高?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,出厂单
,出厂单 价定为60元.该厂为鼓励销售商定购,决定当一次定购量超过100件时,每多定购一件,订购的全部零件的出厂单价就降低0.02元.根据市场调查,销售商一次定购量不会超过500件.
价定为60元.该厂为鼓励销售商定购,决定当一次定购量超过100件时,每多定购一件,订购的全部零件的出厂单价就降低0.02元.根据市场调查,销售商一次定购量不会超过500件. 次定购了450件服装时,该服装厂获得的利润是多少元?
次定购了450件服装时,该服装厂获得的利润是多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com