
 如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点.
如图所示,在空间四边形ABCD中,E、F分别是AB、BC的中点,G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,求证:直线EH,FG和BD共点. 分析 由已知得EF与GH平行且不相等,从而E、F、G、H四点共面,且EH∩FG=O,由此利用公理二能证明直线EH,FG和BD共点.
解答 证明:∵在空间四边形ABCD中,E、F分别是AB、BC的中点,
G、H分别是CD、DA上的点,且DH=$\frac{1}{3}$AD,DG=$\frac{1}{3}$DC,
∴GH∥AC,且GH=$\frac{1}{3}$AC,
EF∥AC,且EF=$\frac{1}{2}AC$,
∴EF与GH平行且不相等,
∴E、F、G、H四点共面,∴EH∩FG=O,如图,
∵E,H∈平面ABD,F,G∈平面BDC,平面ABD∩平面BDC=BD,
∴O∈BD,∴直线EH,FG和BD共点.
点评 本题考查三线共点的证明,是基础题,解题时要认真审题,注意空间思维能力的培养.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
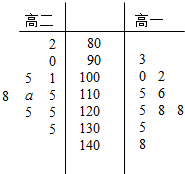 高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)
高三学生小周把自己在高二时的10次数学考试成绩和高三时的10次数学考试成绩(试卷总分150分)进行统计,统计数据用茎叶图表示(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.
角α和β的顶点为平面直角坐标系的原点,始边都与x轴的正半轴重合,终边分别与单位圆(半径为1)相交于点P、Q两点,已知Q点也在射线y=-$\frac{4}{3}$x(x<0)上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(2)<2f(3) | B. | 3f(3)>4f(4) | C. | 3f(4)<4f(3) | D. | f(2)<2f(1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com