
【题目】在讨论勾股定理的过程中,《九章算术》提供了许多整勾股数,如![]() ,等等.其中最大的数称为“弦数”,后人在此基础上进一步研究,得到如下规律:若勾股数组中的某一个数
,等等.其中最大的数称为“弦数”,后人在此基础上进一步研究,得到如下规律:若勾股数组中的某一个数![]() 是确定的奇数(大于1),把它平方后拆成相邻的两个整数,那么奇数与这两个整数构成一组勾股数,若勾股数组中的某一个数
是确定的奇数(大于1),把它平方后拆成相邻的两个整数,那么奇数与这两个整数构成一组勾股数,若勾股数组中的某一个数![]() 是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1所得到的两个整数和这个偶数构成一组勾股数.由此得到的这种勾股数称之为“由
是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1所得到的两个整数和这个偶数构成一组勾股数.由此得到的这种勾股数称之为“由![]() 生成的一组勾股数”.若“由17生成的这组勾股数”的“弦数”为
生成的一组勾股数”.若“由17生成的这组勾股数”的“弦数”为![]() ,“由20生成的这组勾股数”的“弦数”为
,“由20生成的这组勾股数”的“弦数”为![]() ,则
,则![]() ____________.
____________.
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】某娱乐节目参赛选手分初赛培训、复赛三个阶段选拔,将50位参选手的初赛成绩(总分150分)分成[90,100),[100,110),[110,120),[120,130),[130,140)5组进行统计,得到如图所示的频率分布直方图.
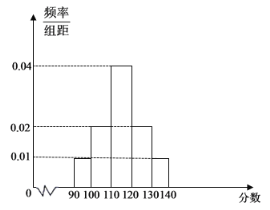
(1)根据频率分析直方图,估算这50个选手初赛成绩的平均分,若节日组规定成绩大于或等于120分的选手可获得节目组组织的培训资格,120分以下(不包括120)的则被淘汰,求这50个人中获得培训资格的人数;
(2)节目组从获得培训资格的人员中选拔部分人员进入复赛.为增加节目的娱乐性,节目组提供了以下两种进入复赛的方式(每位选手只能选择其中一种)
第一种方式:利用分层抽样的方法抽取6名选手参加复赛;
第二种方式:每人最多有5次答题机会,累计答对3题或答错3题终止答题,答对3题可参加复赛
①已知甲的初赛成绩在[120,130)内,他答对每一个问题的概率为![]() ,并且互相之间没有影响甲要想参加复赛,选择那种方式更有利?
,并且互相之间没有影响甲要想参加复赛,选择那种方式更有利?
②若甲选择第二种方式,求他在答题过程中答题个数X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 点在底面
点在底面![]() 内的射影
内的射影![]() 在线段
在线段![]() 上,且
上,且![]() ,
, ![]() ,M在线段
,M在线段![]() 上,且
上,且![]() .
.
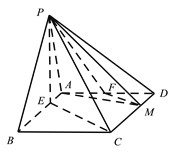
(Ⅰ)证明: ![]() 平面
平面![]() ;
;
(Ⅱ)在线段AD上确定一点F,使得平面![]() 平面PAB,并求三棱锥
平面PAB,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年5月20日以来,广东自西北到东南出现了一次明显降雨.为了对某地的降雨情况进行统计,气象部门对当地20日~28日9天内记录了其中100小时的降雨情况,得到每小时降雨情况的频率分布直方图如下:
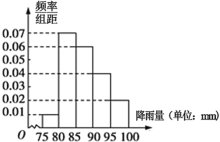
若根据往年防汛经验,每小时降雨量在![]() 时,要保持二级警戒,每小时降雨量在
时,要保持二级警戒,每小时降雨量在![]() 时,要保持一级警戒.
时,要保持一级警戒.
(1)若以每组的中点代表该组数据值,求这100小时内每小时的平均降雨量;
(2)若从记录的这100小时中按照警戒级别采用分层抽样的方法抽取10小时进行深度分析.再从这10小时中随机抽取3小时,求抽取的这3小时中属于一级警戒时间的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年9月15中秋节(农历八月十五)到来之际,某月饼销售企业进行了一项网上调查,得到如下数据:
男 | 女 | 合计 | |
喜欢吃月饼人数(单位:万人) | 50 | 40 | 90 |
不喜欢吃月饼人数(单位:万人) | 30 | 20 | 50 |
合计 | 80 | 60 | 140 |
为了进一步了解中秋节期间月饼的消费量,对参与调查的喜欢吃月饼的网友中秋节期间消费月饼的数量进行了抽样调查,得到如下数据:

已知该月饼厂所在销售范围内有30万人,并且该厂每年的销售份额约占市场总量的35%.
(1)试根据所给数据分析,能否有![]() 以上的把握认为,喜欢吃月饼与性别有关?
以上的把握认为,喜欢吃月饼与性别有关?
参考公式与临界值表: ,
,
其中:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
(2)若忽略不喜欢月饼者的消费量,请根据上述数据估计:该月饼厂恰好生产多少吨月饼恰好能满足市场需求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月24日国家统计局在庆祝中华人民共和国成立70周年活动新闻中心举办新闻发布会指出,1952年~2018年,我国GDP查679.1亿元跃升至90.03万亿元,实际增长174倍;人均GDP从119元提高到6.46万元,实际增长70倍.全国各族人民,砥砺奋进,顽强拼搏,实现了经济社会的跨越式发展.如图是全国2010年至2018年GDP总量![]() (万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
(万亿元)的折线图.注:年份代码1~9分别对应年份2010~2018.
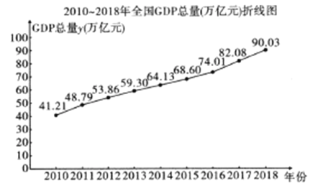
(1)由折线图看出,可用线性回归模型拟合![]() 与年份代码
与年份代码![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
的回归方程(系数精确到0.01),并预测2021年全国GDP的总量.
附注:参考数据:![]() .
.
参考公式:相关系数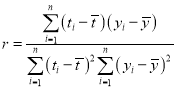 ;
;
回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为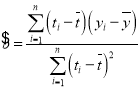 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四个命题:其中所有假命题的序号是_______.
①命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ;
;
②将函数![]() 的图像向右平移
的图像向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图像;
的图像;
③幂函数![]() 在
在![]() 上是减函数,则实数
上是减函数,则实数![]() ;
;
④函数![]() 有两个零点.
有两个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点 ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若点![]() 与点
与点![]() 均在椭圆
均在椭圆![]() 上,且
上,且![]() 关于原点对称,问:椭圆上是否存在点
关于原点对称,问:椭圆上是否存在点![]() (点
(点![]() 在一象限),使得
在一象限),使得![]() 为等边三角形?若存在,求出点
为等边三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com