
分析 根据充分必要条件的定义分别对①②③④进行判断即可.
解答 解:①“若x2+y2=0,则x、y全为0”的逆命题是真命题,
②“若x、y都是偶数,则x+y是偶数”的否命题是“若x、y不都是偶数,则x+y不是偶数”,是假命题,
③命题p:抛物线y2=8x的准线方程是x=-$\frac{p}{2}$=-2,是真命题,
命题q:半径为2,母线长为3的圆锥侧面积为S=π×2×3=6π,是真命题,
故p∧q是真命题,
④已知b?α;若“a∥b”,则“a∥α或a?α”,
∴“a∥b”不是“a∥α”的充分条件,
故答案为:③.
点评 本题考查了充分必要条件,考查抛物线、椎体的体积公式问题、命题之间的关系以及直线和平面的位置关系,是一道综合题.


科目:高中数学 来源: 题型:解答题
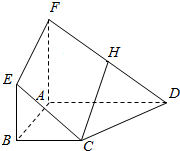 如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.
如图,四边形ABEF与四边形ABCD都是梯形,BC∥AD,BC=$\frac{1}{2}$AD,BE∥AF,BE=$\frac{1}{2}$AF,H是FD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
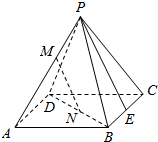 如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.
如图,已知P是正方形ABCD外一点,M,N分别是PA,BD上的点,且$\frac{PM}{MA}$=$\frac{BN}{ND}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | [0,+∞) | C. | (-∞,+∞) | D. | [1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com