
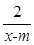 在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若
在区间(1,+∞)上是减函数;命题q:x1,x2是方程x2-ax-2=0的两个实根,且不等式m2+5m-3≥|x1-x2|对任意的实数a∈[-1,1]恒成立.若 p∧q为真,试求实数m的取值范围.
p∧q为真,试求实数m的取值范围. 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com