
【题目】已知函数![]()
(Ⅰ)如果曲线![]() 在点
在点![]() 处的切线的斜率是
处的切线的斜率是![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() ,
,![]() 时,求证:
时,求证:![]() ;
;
(Ⅲ)若![]() 存在单调递增区间,请直接写出
存在单调递增区间,请直接写出![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)见解析;(Ⅲ)
;(Ⅱ)见解析;(Ⅲ)![]()
【解析】
(Ⅰ)由![]() 即可解出
即可解出![]() ;(Ⅱ)对
;(Ⅱ)对![]() 进行二次求导,通过二次求导所得导函数恒正,得到
进行二次求导,通过二次求导所得导函数恒正,得到![]() 单调递增;根据零点存在定理可知在
单调递增;根据零点存在定理可知在![]() 上,
上,![]() 存在零点;根据导函数符号得到
存在零点;根据导函数符号得到![]() 单调性,从而确定
单调性,从而确定![]() 最大值为
最大值为![]() ,则结论可证;(III)将问题转化为存在
,则结论可证;(III)将问题转化为存在![]() ,使得
,使得![]() ,通过分离变量将问题转化为
,通过分离变量将问题转化为![]() 与
与![]() 最值的比较;在
最值的比较;在![]() 时求
时求![]() 的最小值;
的最小值;![]() 时求
时求![]() 的最大值,由于最值点无法取得,结合洛必达法则求得极限值;从而可得
的最大值,由于最值点无法取得,结合洛必达法则求得极限值;从而可得![]() 的取值范围.
的取值范围.
(Ⅰ)由题意知:![]()
则![]() ,即
,即![]()
![]()
(Ⅱ)当![]() 时,
时,![]() img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/15/08/7528bcf4/SYS201908150803096317375479_DA/SYS201908150803096317375479_DA.019.png" width="125" height="23" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
img src="http://thumb.zyjl.cn/questionBank/Upload/2019/08/15/08/7528bcf4/SYS201908150803096317375479_DA/SYS201908150803096317375479_DA.019.png" width="125" height="23" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />
令![]()
![]()
![]()
![]()
因此![]() 恒成立
恒成立
![]() 当
当![]() 时,
时,![]() 单调递增
单调递增
又![]() ,
,![]()
![]() 存在唯一的
存在唯一的![]() ,使得
,使得![]()
列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极小值 |
|
|
当![]() 时,
时,![]()
![]() 当
当![]() ,
,![]() 时,
时,![]()
(Ⅲ)由题意可知,存在![]() ,使得
,使得![]()
当![]() 时,
时,![]() ,不合题意;
,不合题意;
当![]() 时,
时,![]()
令![]() ,则
,则![]()
当![]() 时,
时,![]() ,则
,则![]() 单调递减;
单调递减;![]() 时,
时,![]() ,则
,则![]() 单调递增
单调递增
可得![]() 时,函数
时,函数![]() 取得极小值即最小值
取得极小值即最小值 ![]()
当![]() 时,
时,![]()
当![]() 时,
时,![]() ,则
,则![]() 单调递减.
单调递减.
又![]() 时,
时,![]()
![]() .
.
综上可得:![]()


 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:
【题目】已知点P(x,y)在△ABC的边界和内部运动,其中A(1,0),B(2,1),C(4,4).若z=2x-y的最小值为M,最大值为N.
(1)求M,N;
(2)若m+n=M,m>0,n>0,求![]() 的最小值,并求此时的m,n的值;
的最小值,并求此时的m,n的值;
(3)若m+n+mn=N,m>0,n>0,求mn的最大值和m+n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知圆![]() 的圆心在直线
的圆心在直线![]() 上,且过点
上,且过点![]() ,与直线
,与直线![]() 相切.
相切.
(![]() )求圆
)求圆![]() 的方程.
的方程.
(![]() )设直线
)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点.求实数
两点.求实数![]() 的取值范围.
的取值范围.
(![]() )在(
)在(![]() )的条件下,是否存在实数
)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c.且满足4cos2![]() cos2(B+C)
cos2(B+C)![]() .
.
(1)求角A;
(2)若△ABC的面积为![]() ,周长为8,求a.
,周长为8,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以原点
为参数).以原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的直角坐标方程与圆
的直角坐标方程与圆![]() 的普通方程;
的普通方程;
(2)点![]() 为直线
为直线![]() 上的一动点,过点
上的一动点,过点![]() 作直线
作直线![]() 与圆
与圆![]() 相切于点
相切于点![]() ,求四边形
,求四边形![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国华南沿海地区是台风登陆频繁的地区,为统计地形地貌对台风的不同影响,把华南沿海分成东西两区,对台风的强度按风速划分为:风速不小于30米/秒的称为强台风,风速小于30米/秒的称为风暴,下表是2014年对登陆华南地区的15次台风在东西两部的强度统计:

(1)根据上表,计算有没有99%以上的把握认为台风强度与东西地域有关;
(2)2017年8月23日,“天鸽”在深圳登陆,造成深圳特大风暴,如图所示的茎叶图统计了深圳15块区域的风速.(十位数为茎,个位数为叶)
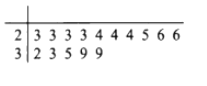
①任取2个区域进行统计,求取到2个区域风速不都小于25的概率;
②任取3个区域进行统计, ![]() 表示“风速达到强台风级别的区域个数”,求
表示“风速达到强台风级别的区域个数”,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附: 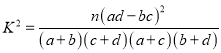 ,其中
,其中![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某医院为促进行风建设,拟对医院的服务质量进行量化考核,每个患者就医后可以对医院进行打分,最高分为100分.上个月该医院对100名患者进行了回访调查,将他们按所打分数分成以下几组:第一组![]() ,第二组
,第二组![]() ,第三组
,第三组![]() ,第四组
,第四组![]() ,第五组
,第五组![]() ,得到频率分布直方图,如图所示.
,得到频率分布直方图,如图所示.
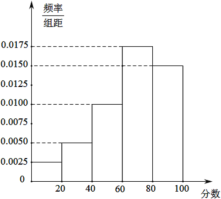
(1)求所打分数不低于60分的患者人数;
(2)该医院在第二三组患者中按分层抽样的方法抽取6名患者进行深入调查,之后将从这6人中随机抽取2人聘为医院行风监督员,求行风监督员来自不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 的底面ABCD是边长为a的菱形,
的底面ABCD是边长为a的菱形,![]() 面ABCD,
面ABCD,![]() ,E,F分别是CD,PC的中点.
,E,F分别是CD,PC的中点.

(1)求证:平面![]() 平面PAB;
平面PAB;
(2)M是PB上的动点,EM与平面PAB所成的最大角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com