
| A. | $[-\frac{{\sqrt{3}}}{2},\frac{{\sqrt{3}}}{2}]$ | B. | $[-\sqrt{3},\sqrt{3}]$ | C. | [-2,2] | D. | [-1,1] |
分析 通过两角差的余弦函数化简函数的表达式,利用两角差的正弦函数化为一个角的一个三角函数的形式,求出函数的值域.
解答 解:∵f(x)=sinx-cos(x-$\frac{π}{6}$)
=sinx-$\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx
=$\frac{1}{2}$sinx-$\frac{\sqrt{3}}{2}$cosx
=sin(x-$\frac{π}{3}$).
∴函数f(x)=sinx-cos(x-$\frac{π}{6}$)的值域为[-1,1].
故选:D.
点评 本题考查三角函数中的恒等变换应用,正弦函数的定义域和值域,考查计算能力,利用两角差的正弦函数化为一个角的一个三角函数的形式是关键,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
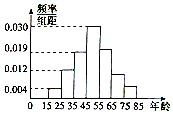 某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了100位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.
某购物中心为了了解顾客使用新推出的某购物卡的顾客的年龄分布情况,随机调查了100位到购物中心购物的顾客年龄,并整理后画出频率分布直方图如图所示,年龄落在区间[55,65),[65,75),[75,85]内的频率之比为4:2:1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2$\sqrt{3}$,4) | B. | [-2$\sqrt{3}$,4] | C. | [-4,4] | D. | [-4,2$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{25}$ | B. | -$\frac{7}{25}$ | C. | $\frac{25}{7}$ | D. | -$\frac{25}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $z=\frac{1}{5}x-y$ | B. | z=3x+y | C. | $z=-\frac{1}{5}x-y$ | D. | z=3x-y |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | [$\frac{1}{e}$,+∞) | C. | (-∞,$\frac{1}{e}$] | D. | [e,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com