
【题目】已知椭圆C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,其内接正方形的面积为4.
,其内接正方形的面积为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设M为椭圆C的右顶点,过点![]() 且斜率不为0的直线l与椭圆C相交于P,Q两点,记直线PM,QM的斜率分别为k1,k2,求证:k1k2为定值.
且斜率不为0的直线l与椭圆C相交于P,Q两点,记直线PM,QM的斜率分别为k1,k2,求证:k1k2为定值.
【答案】(Ⅰ)![]() +
+![]() =1(Ⅱ)见解析
=1(Ⅱ)见解析
【解析】
(Ⅰ)由椭圆的离心率可以得到![]() 的关系,结合
的关系,结合![]() ,可知
,可知![]() 的关系,
的关系,
由对称性可得,可求椭圆内接正方形位于第一象限顶点的坐标,代入椭圆方程中,求出![]() 的值。
的值。
(Ⅱ)设了直线方程,与椭圆方程联立,得到一个一元二次方程,求出k1k2的表达式,利用一元二次方程根与系数的关系,对表达式进行化简求值。
解:(Ⅰ)∵e=![]() =
=![]() ,
,
∴a=![]() c,即a2=2b2,①,
c,即a2=2b2,①,
由对称性可得,椭圆内接正方形位于第一象限顶点的坐标为(x0,y0),
∴4x02=4,x0=1,
∴![]() +
+![]() =1,②,
=1,②,
由①②解得a=![]() ,b=
,b=![]() ,
,
∴椭圆C的标准方程为![]() +
+![]() =1.
=1.
(Ⅱ)由(Ⅰ)可知M(![]() ,0),依题意得直线l的斜率存在,设其方程为y=k(x-3
,0),依题意得直线l的斜率存在,设其方程为y=k(x-3![]() ),
),
设P(x1,y1),Q(x2,y2),(x1,x2≠![]() ),联立方程
),联立方程![]() ,消去y并整理可得
,消去y并整理可得
![]() ∴x1+x2=
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴k1k2=![]()
![]() =
=![]()
![]() =
=![]() =
=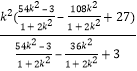 =
=![]() =1,
=1,
∴k1k2=1


科目:高中数学 来源: 题型:
【题目】某中学为了组建一支业余足球队,在高一年级随机选取50名男生测量身高,发现被测男生的身高全部在![]() 到
到![]() 之间,将测量结果按如下方式分成六组:第1组
之间,将测量结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组得到的频率分布直方图,以频率近似概率.
,如图是按上述分组得到的频率分布直方图,以频率近似概率.
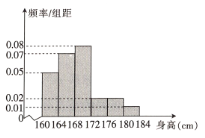
(1)若学校要从中选1名男生担任足球队长,求被选取的男生恰好在第5组或第6组的概率;
(2)试估计该校高一年级全体男生身高的平均数(同一组中的数据用该组区间的中点值代表)与中位数;
(3)现在从第5与第6组男生中选取两名同学担任守门员,求选取的两人中最多有1名男生来自第5组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的内角
的内角![]() 、
、![]() 、
、![]() 的对边分别为
的对边分别为![]() 、
、![]() 、
、![]() ,
,![]() 为
为![]() 内一点,若分别满足下列四个条件:
内一点,若分别满足下列四个条件:
①![]() ;
;
②![]() ;
;
③![]() ;
;
④![]() ;
;
则点![]() 分别为
分别为![]() 的( )
的( )
A.外心、内心、垂心、重心B.内心、外心、垂心、重心
C.垂心、内心、重心、外心D.内心、垂心、外心、重心
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,两铁路线垂直相交于站![]() ,若已知
,若已知![]() 千米,甲火车从
千米,甲火车从![]() 站出发,沿
站出发,沿![]() 方向以
方向以![]() 千米
千米![]() 小时的速度行驶,同时乙火车从
小时的速度行驶,同时乙火车从![]() 站出发,沿
站出发,沿![]() 方向,以
方向,以![]() 千米
千米![]() 小时的速度行驶,至
小时的速度行驶,至![]() 站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
站即停止前行(甲车扔继续行驶)(两车的车长忽略不计).
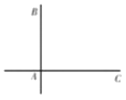
(1)求甲、乙两车的最近距离(用含![]() 的式子表示);
的式子表示);
(2)若甲、乙两车开始行驶到甲,乙两车相距最近时所用时间为![]() 小时,问
小时,问![]() 为何值时
为何值时![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com