
【题目】已知定义在R上的单调函数f(x)满足对任意的x1 , x2 , 都有f(x1+x2)=f(x1)+f(x2)成立.若正实数a,b满足f(a)+f(2b﹣1)=0,则 ![]() 的最小值为 .
的最小值为 .
科目:高中数学 来源: 题型:
【题目】现有4种不同颜色要对如图所示的四个部分进行着色,要求有公共边界的两部分不能用同一种颜色,则不同的着色方法共有( )

A. 144种 B. 72种 C. 64种 D. 84种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,内角A,B,C的对边分别为a,b,c,2sin2 ![]() =sinC+1.
=sinC+1.
(Ⅰ)求角C的大小;
(Ⅱ)若a= ![]() ,c=1,求△ABC的面积.
,c=1,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过抛物线y=![]() 焦点F的直线交抛物线于A,B两点,点C在直线y=-1上,若△ABC为正三角形,则其边长为
焦点F的直线交抛物线于A,B两点,点C在直线y=-1上,若△ABC为正三角形,则其边长为
A. 11 B. 13 C. 14 D. 12
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (a>b>0)的左、右焦点分别为F1,F2,且离心率为
(a>b>0)的左、右焦点分别为F1,F2,且离心率为![]() ,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
,M为椭圆上任意一点,当∠F1MF2=90°时,△F1MF2的面积为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点A是椭圆C上异于椭圆顶点的一点,延长直线AF1,AF2分别与椭圆交于点B,D,设直线BD的斜率为k1,直线OA的斜率为k2,求证:k1·k2等于定值.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(Ⅰ)由题意可求得![]() ,则
,则![]() ,椭圆
,椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
当直线![]() 的斜率不存在或直线
的斜率不存在或直线![]() 的斜率不存在时,
的斜率不存在时,![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方程,结合韦达定理计算可得直线
,联立直线方程与椭圆方程,结合韦达定理计算可得直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() .综上可得:直线
.综上可得:直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() .
.
(Ⅰ)设![]() 由题
由题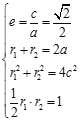 ,
,
解得![]() ,则
,则![]() ,
,![]() 椭圆
椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,当直线
,当直线![]() 的斜率不存在时,
的斜率不存在时,
设![]() ,则
,则![]() ,直线
,直线![]() 的方程为
的方程为![]() 代入
代入![]() ,
,
可得![]()
![]() ,
,![]() ,则
,则![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为 ,直线
,直线![]() 的斜率为
的斜率为![]() ,
,
![]() ,
,
当直线![]() 的斜率不存在时,同理可得
的斜率不存在时,同理可得![]() .
.
当直线![]() 、
、![]() 的斜率存在时,
的斜率存在时,![]() 设直线
设直线![]() 的方程为
的方程为![]() ,
,
则由 消去
消去![]() 可得:
可得:![]() ,
,
又![]() ,则
,则![]() ,代入上述方程可得:
,代入上述方程可得:
![]() ,
,![]() ,
,
则![]()
![]() ,
,
设直线![]() 的方程为
的方程为![]() ,同理可得
,同理可得![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,
,![]()
 .
.
所以,直线![]() 与
与![]() 的斜率之积为定值
的斜率之积为定值![]() ,即
,即![]() .
.
【点睛】
(1)解答直线与椭圆的题目时,时常把两个曲线的方程联立,消去x(或y)建立一元二次方程,然后借助根与系数的关系,并结合题设条件建立有关参变量的等量关系.
(2)涉及到直线方程的设法时,务必考虑全面,不要忽略直线斜率为0或不存在等特殊情形.
【题型】解答题
【结束】
21
【题目】已知函数f(x)=(x+b)(![]() -a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
-a),(b>0),在(-1,f(-1))处的切线方程为(e-1)x+ey+e-1=0.
(Ⅰ)求a,b;
(Ⅱ)若方程f(x)=m有两个实数根x1,x2,且x1<x2,证明:x2-x1≤1+![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有人在路边设局,宣传牌上写有“掷骰子,赢大奖”.其游戏规则是这样的:你可以在1,2,3,4,5,6点中任选一个,并押上赌注![]() 元,然后掷1颗骰子,连续掷3次,若你所押的点数在3次掷骰子过程中出现1次,2次,3次,那么原来的赌注仍还给你,并且庄家分别给予你所押赌注的1倍,2倍,3倍的奖励.如果3次掷骰子过程中,你所押的点数没出现,那么你的赌注就被庄家没收.
元,然后掷1颗骰子,连续掷3次,若你所押的点数在3次掷骰子过程中出现1次,2次,3次,那么原来的赌注仍还给你,并且庄家分别给予你所押赌注的1倍,2倍,3倍的奖励.如果3次掷骰子过程中,你所押的点数没出现,那么你的赌注就被庄家没收.
(1)求掷3次骰子,至少出现1次为5点的概率;
(2)如果你打算尝试一次,请计算一下你获利的期望值,并给大家一个正确的建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个圆锥的底面半径为1,高为3,在圆锥中有一个半径为x的内接圆柱.

(1)试用x表示圆柱的高;
(2)当x为何值时,圆柱的侧面积最大,最大侧面积是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com