
已知向量 ,
, ,函数
,函数 ,
, 三个内角
三个内角 的对边分别为
的对边分别为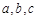 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)若
 ,求
,求 的面积
的面积 .
.
(1)函数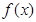 的单调增区间为
的单调增区间为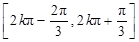
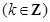 .
.
(2) 的面积
的面积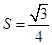 .
.
解析试题分析:(1)根据平面向量的数量积,应用和差倍半的三角函数公式,将 化简为
化简为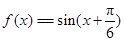 ,讨论函数的单调性;
,讨论函数的单调性;
(2) 本题解答可有两种思路,在利用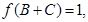 得到
得到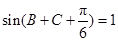 ,
,
求得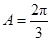 后,一是可应用正弦定理
后,一是可应用正弦定理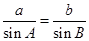 ,得到
,得到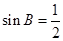 ,
,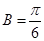 或者
或者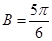 根据
根据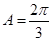 为钝角,确定
为钝角,确定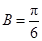 ,得
,得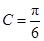 ;二是应用余弦定理,
;二是应用余弦定理, ,得
,得 ,
,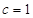 或
或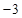 (舍去),进一步确定
(舍去),进一步确定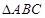 的面积
的面积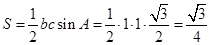 .
.
试题解析:(1)由题意得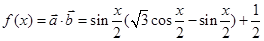
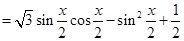
=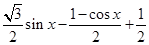 =
=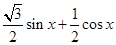
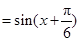 , 3分
, 3分
令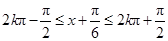

解得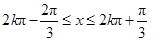

所以函数 的单调增区间为
的单调增区间为
 . 6分
. 6分
(2) 解法一:因为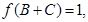 所以
所以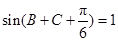 ,
,
又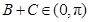 ,
,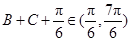 ,
,
所以 ,所以
,所以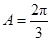 , 8分
, 8分
由正弦定理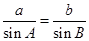 把
把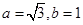 代入,得到
代入,得到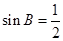 10分
10分
得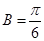 或者
或者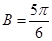 ,因为
,因为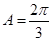 为钝角,所以
为钝角,所以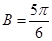 舍去
舍去
所以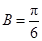 ,得
,得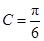 .
.
所以,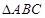 的面积
的面积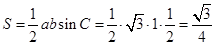 . 12分
. 12分
解法二:同上(略)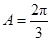 , 8分
, 8分
由余弦定理, ,得
,得 ,
,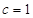 或
或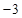 (舍去)10分
(舍去)10分
所以,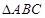 的面积
的面积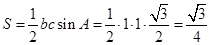 . 12分
. 12分
考点:平面向量的数量积,和差倍半的三角函数,正弦定理、余弦定理的应用,三角形面积公式.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:解答题
某人在汽车站M的北偏西20°的方向上的A处(如图所示),观察到C处有一辆汽车沿公路向M站行驶,公路的走向是M站的北偏东40°.开始时,汽车到A处的距离为31km,汽车前进20km后,到A处的距离缩短了10km.问汽车还需行驶多远,才能到达汽车站M?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,已知sinAsinB+sinBsinC+cos =2B=1.
(1)求证:a,b,c成等差数列;
(2)若C= ,求
,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知m=(2cos x+2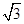 sin x,1),n=(cos x,-y),且m⊥n.
sin x,1),n=(cos x,-y),且m⊥n.
(1)将y表示为x的函数f(x),并求f(x)的单调递增区间;
(2)已知a,b,c分别为△ABC的三个内角A,B,C对应的边长,若f =3,且a=2,b+c=4,求△ABC的面积.
=3,且a=2,b+c=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,a,b,c分别为角A,B,C的对边.已知a=1,b=2,sinC= (其中C为锐角).
(其中C为锐角).
(1)求边c的值.
(2)求sin(C-A)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,若acos2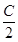 +ccos2
+ccos2 =
= b.
b.
(1)求证:a,b,c成等差数列;
(2)若∠B=60°,b=4,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知△ABC的内角为A、B、C,其对边分别为a、b、c,B为锐角,向量m=(2sin B,- ),n=
),n= ,且m∥n
,且m∥n
(1)求角B的大小;
(2)如果b=2,求S△ABC的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com