练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线的倾斜角 的余弦值 ，则此直线的斜率是（ ）．
    A.
    B.－
    C.
    D.±

    【答案】A
    【解析】解答：因为倾斜角 的余弦值为 ，所以直线的斜率为 ，答案选A. 分析：本题主要考查了直线的斜率与倾斜角之间的关系，解决问题的关键是根据有关定义进行准确计算即可.
    【考点精析】本题主要考查了直线的倾斜角和直线的斜率的相关知识点，需要掌握当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°；一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在空间直角坐标系中，已知A（3，0，1）和B（1，0，－3），试问
    （1）在y轴上是否存在点M，满足 ？
    （2）在y轴上是否存在点M，使△MAB为等边三角形？若存在，试求出点M坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|x|﹣|2x﹣1|，记f（x）＞﹣1的解集为M．
    （1）求M；
    （2）已知a∈M，比较a2﹣a+1与 的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】直线 经过 两点，那么直线 的倾斜角的取值范围（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知cos = ，cos cos = ，cos cos cos = ，…，根据这些结果，猜想出的一般结论是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆： （）过点，且椭圆的离心率为．

    （1）求椭圆的方程；

    （2）若动点在直线上，过作直线交椭圆于两点，且为线段中点，再过作直线．求直线是否恒过定点，如果是则求出该定点的坐标，不是请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】三棱锥P﹣ABC的高为PH，若三个侧面两两垂直，则H为△ABC的（ ）
    A.内心
    B.外心
    C.垂心
    D.重心

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在直三棱柱ABC﹣A1B1C1中，底面△ABC为等腰直角三角形，∠B=90°，D为棱BB1上一点，且平面DA1C⊥平面AA1C1C．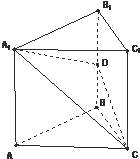
    （1）求证：D点为棱BB1的中点；
    （2）判断四棱锥A1﹣B1C1CD和C﹣A1ABD的体积是否相等，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知集合M={x|≤1}，N={x|y=lg（1﹣x）}，则下列关系中正确的是（　　）
    A.（RM）∩N=
    B.M∪N=R
    C.MN
    D.（RM）∪N=R

    查看答案和解析>>

    同步练习册答案