
分析 由条件利用函数y=Asin(ωx+φ)的图象和性质、以及它的图象变换规律,正弦函数的周期性和单调性,得出结论.
解答 解:对于函数f(x)=$\sqrt{3}$sin(2x-$\frac{2}{3}$π),它的最小正周期为$\frac{2π}{2}$=π,故排除①.
函数f(x)的振幅为$\sqrt{3}$,故②正确.
函数的图象是由y=$\sqrt{3}$sin2x图象向右平移$\frac{π}{3}$得到的,故③不正确.
对于函数f(x),令2kπ-$\frac{π}{2}$≤2x-$\frac{2π}{3}$≤2kπ+$\frac{π}{2}$,求得kπ+$\frac{π}{12}$≤2≤kπ+$\frac{7π}{12}$,故它的一个单调递增区间为[$\frac{π}{12}$,$\frac{7π}{12}$].
故答案为:②④.
点评 本题主要考查函数y=Asin(ωx+φ)的图象和性质、以及它的图象变换规律,正弦函数的周期性和单调性,属于基础题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:选择题
| A. | 7秒钟 | B. | 8秒钟 | C. | 9秒钟 | D. | 10秒钟 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 认为作业多 | 认为作业不多 | |
| 喜欢玩电脑游戏 | 18 | 9 |
| 不喜欢玩电脑游戏 | 8 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
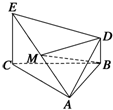 如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,EC=CA=2BD,M是EA的中点.求证:
如图所示,△ABC为正三角形,EC⊥平面ABC,BD∥CE,EC=CA=2BD,M是EA的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com