
【题目】在直角坐标系xoy中,直线l经过点P(﹣1,0),其倾斜角为α,在以原点O为极点,x轴非负半轴为极轴的极坐标系中(取相同的长度单位),曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0. (Ⅰ)若直线l与曲线C有公共点,求α的取值范围;
(Ⅱ)设M(x,y)为曲线C上任意一点,求x+y的取值范围.
【答案】解:(Ⅰ)∵曲线C的极坐标方程为ρ2﹣6ρcosθ+1=0,∴曲线C的直角坐标方程为x2+y2﹣6x+1=0 ∵直线l经过点P(﹣1,0),其倾斜角为α,∴直线l的参数方程为 ![]() (t为参数)
(t为参数)
将 ![]() ,代入x2+y2﹣6x+1=0整理得t2﹣8tcosα+8=0
,代入x2+y2﹣6x+1=0整理得t2﹣8tcosα+8=0
∵直线l与曲线C有公共点,∴△=64cos2α﹣32≥0即 ![]() 或
或 ![]()
∵α∈[0,π)∴α的取值范围是 ![]()
(Ⅱ)曲线C的直角坐标方程为x2+y2﹣6x+1=0可化为(x﹣3)2+y2=8
其参数方程为 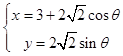 (θ为参数)
(θ为参数)
∵M(x,y)为曲线C上任意一点,∴ ![]()
∴x+y的取值范围是[﹣1,7].
【解析】(Ⅰ)由直线l经过点P(﹣1,0),且倾斜角为α,可得直线l的参数方程,利用互化公式可得C的直角坐标方程.由直线l与曲线C有公共点,可得△=64cos2α﹣32≥0,解出即可得出的取值范围; (Ⅱ)设M(x,y)为曲线C上任意一点,利用参数方程为 ![]() (θ为参数),结合三角函数知识求x+y的取值范围.
(θ为参数),结合三角函数知识求x+y的取值范围.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)=x﹣a(x+1)ln(x+1),(x>﹣1,a≥0)
(Ⅰ)求f(x)的单调区间;
(Ⅱ)当a=1时,若方程f(x)=t在 ![]() 上有两个实数解,求实数t的取值范围;
上有两个实数解,求实数t的取值范围;
(Ⅲ)证明:当m>n>0时,(1+m)n<(1+n)m .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]()
![]() .
.
(1)求函数f(x)的值域;
(2)已知锐角△ABC的两边长分别为函数f(x)的最大值与最小值,且△ABC的外接圆半径为 ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x)满足f(x)+f(x+5)=16,当x∈(﹣1,9)时,f(x)=x2﹣2x , 则函数f(x)在[0,2016]上的零点个数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() (x
(x![]() R),g(x)=2a-1
R),g(x)=2a-1
(1)求函数f(x)的单调区间与极值.
(2)若f(x)≥g(x)对![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在每年的春节后,某市政府都会发动公务员参加植树活动,林业部门在植树前,为了保证树苗的质量,将在植树前对树苗进行检测,现从同一种树的甲、乙两批树苗中各抽测了10株树苗,量出它们的高度如下(单位:厘米):
甲:37,21,31,20,29,19,32,23,25,33; 乙:10,30,47,27,46,14,26,10,44,46.
(1)你能用适当的统计图表示上面的数据吗?
(2)根据你所画的统计图,对甲,乙两种树苗的高度作比较,写出两个统计结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com