
| A. | $y=sin(2x+\frac{π}{2})$ | B. | $y=sin(2x+\frac{π}{6})$ | C. | $y=sin(2x+\frac{2π}{3})$ | D. | y=sin2x |
科目:高中数学 来源: 题型:解答题
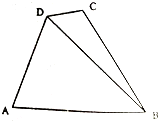 随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°
随州市某处有如图所示的A、B、C、D四个景点,目前AD、AB、DC之间已修建公路,市政府为了更好发展随州的旅游产业,决定新修建两条公路用以连接B、D两景点和B、C两景点.现测得AD=5km,AB=7km,∠ADB=60°,∠ADC=105°,∠CBD=15°查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AB}$ | B. | $\overrightarrow{DA}$ | C. | $\overrightarrow{BC}$ | D. | $\overrightarrow{0}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 |
| y | 17 | 12 | 7 | 4 |
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b>0 | D. | a<0,b>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )
在一次数学竞赛中,高一•1班30名学生的成绩茎叶图如图所示:若将学生按成绩由低到高编为1-30号,再用系统抽样的方法从中抽取6人,则其中成绩在区间[73,90]上的学生人数为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10种 | B. | 20种 | C. | 30种 | D. | 40种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com