
����Ŀ��ij��ѧ���ڿ�ѧʱ����һ�θ����꼶����ѧ����̸�ᣬ����20�����Ա�У����(1)(2)(3)(4)���ѧ���μӣ����������ѧ�������±���ʾ��
�༶ | ������1�� | ������2�� | ������3�� | ������4�� |
���� | 4 | 6 | 4 | 6 |
(1)����20��ѧ�������ѡ��3��ѧ�����ԣ�����3��ѧ��������������������ͬһ�༶�ĸ��ʣ�
(2)����20��ѧ�������ѡ��3 ��ѧ�����ԣ������Ը�����3����ѧ����Ϊ![]() �����������
�����������![]() �ĸ��ʷֲ��к���ѧ����.
�ĸ��ʷֲ��к���ѧ����.
���𰸡�(1)![]() (2)������.
(2)������.
�������������������1����![]() ��ѧ�����ѡ��
��ѧ�����ѡ��![]() ���ķ�����Ϊ
���ķ�����Ϊ![]() , ѡ��
, ѡ��![]() ��������������������ͬһ�༶�ķ����������ùŵ���ͼ�����ʹ�ʽ��������⣮
��������������������ͬһ�༶�ķ����������ùŵ���ͼ�����ʹ�ʽ��������⣮
(2)��![]() ���ܵ�ȡֵΪ
���ܵ�ȡֵΪ![]() ������������
������������![]() ÿ��ֵ��Ӧ�ĸ��ʣ��г��ֲ��У����ù�ʽ�����ѧ������
ÿ��ֵ��Ӧ�ĸ��ʣ��г��ֲ��У����ù�ʽ�����ѧ������
���������
��1���� 20 ��ѧ�����ѡ�� 3 ���ķ�����Ϊ![]() , ѡ�� 3 ��������������������ͬһ�༶�ķ�����Ϊ
, ѡ�� 3 ��������������������ͬһ�༶�ķ�����Ϊ![]()
�� 3 ��ѧ��������������������ͬһ�༶���¼�Ϊ![]()
����![]()
(2)![]() ���ܵ�ȡֵΪ 0,1,2,3
���ܵ�ȡֵΪ 0,1,2,3
![]() ,
,
![]() .
.
����![]() �ķֲ���Ϊ
�ķֲ���Ϊ
| 0 | 1 | 2 | 3 |
|
|
|
|
|
����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x����x��R������f����x��=4��f��x�������� ![]() ��������y=f��x����y=g��x��ͼ��Ľ���ֱ�Ϊ��x1 �� y1������x2 �� y2������x3 �� y3����������xm �� ym������
��������y=f��x����y=g��x��ͼ��Ľ���ֱ�Ϊ��x1 �� y1������x2 �� y2������x3 �� y3����������xm �� ym������ ![]() ������ú���m��ʽ�ӱ�ʾ����
������ú���m��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ij��2017��4��1����14�յĿ�������ָ������ͼ����������ָ����AQI��С��100��ʾ����������������������ָ������200��ʾ�����ض���Ⱦ��ijͬ־���ѡ��4��1����4��12���е�ijһ�쵽����У���ͣ��3�죮 ��ͬ־���ﵱ�տ��������ض���Ⱦ�ĸ��� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f(x)����![]() x3��x2��(m2��1)x(x��R)������m>0.
x3��x2��(m2��1)x(x��R)������m>0.
(1)��m��1ʱ��������y��f(x)�ڵ�(1��f(1))��������б�ʣ�
(2)�����ĵ��������뼫ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�����C1�IJ�������Ϊ![]() (
(![]() Ϊ����)����������ԭ��OΪ���㣬x��������Ϊ����ļ�����ϵ�У�����C2������2sin ����ֱ��
Ϊ����)����������ԭ��OΪ���㣬x��������Ϊ����ļ�����ϵ�У�����C2������2sin ����ֱ��![]() ������
������![]() (����0)��A(2,0)��
(����0)��A(2,0)��
(1)��C1����ͨ���̻�Ϊ�����귽�̣������A��ֱ��![]() ���о��룻
���о��룻
(2)��ֱ��![]() �ֱ�C1��C2�ڵ�P��Q������APQ�������
�ֱ�C1��C2�ڵ�P��Q������APQ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͳ��ѧ�У�ƫ����ָ����ⶨֵ��ⶨ��ƽ��ֵ֮��ڳɼ�ͳ���У����ǰ�ij��ͬѧ��ij�ƿ��Գɼ���ÿư�ƽ���ֵIJ��ij��ƫ�������Ϊ���˽����ѧ����ƫ���������ѧ����ѧƫ��x(��λ����)������ƫ��y(��λ����)֮��Ĺ�ϵ����ѧ��ƫ�������������ȫ��56λͬѧ�������ȡһ������Ϊ8���������з������õ����ǵ����Ƴɼ�ƫ���������£�
ѧ����� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
��ѧƫ��x | 20 | 15 | 13 | 3 | 2 | ��5 | ��10 | ��18 |
����ƫ��y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | ��0.5 | ��2.5 | ��3.5 |
(1)��֪x��y֮�����������ع�ϵ����y����x�����Իع鷽�̣�
(2)����ο��Ըð���ѧƽ����Ϊ118�֣�����ƽ����Ϊ90.5����Ԥ����ѧ�ɼ�126�ֵ�ͬѧ�������ɼ�.
�ο���ʽ�� 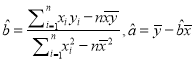 .
.
�ο����ݣ� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ϊ�˹涨��ʱ�����Ҫȷ���ӹ���������ѵ�ʱ�䣬Ϊ�������Ĵ����飬�õ����������£�
����ĸ���x������ | 2 | 3 | 4 | 5 |
�ӹ���ʱ��y��Сʱ�� | 2.5 | 3 | 4 | 4.5 |
��1���ڸ���������ϵ�л����������ݵ�ɢ��ͼ��
��2�����y����x�����Իع鷽��![]() ��
��
��3����Ԥ��ӹ�10�������Ҫ����ʱ��.
�ο���ʽ���ع�ֱ��![]() ��
��
���� ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����{an}��ǰn���ΪSn �� ��a1=1����Sn=tan�� ![]() ������n��N*��
������n��N*��
��1����ʵ��t��ֵ������{an}��ͨ�ʽ��
��2��������{bn}����bn=log3a2n �� ������{ ![]() }��ǰn���Tn ��
}��ǰn���Tn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a,b,c��Ϊʵ������![]() ��
��![]() ��
��![]() ��
��
���÷�֤��֤����a��b��c��������һ������0.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com