
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,ccosA+ ![]() csinA﹣b﹣a=0.
csinA﹣b﹣a=0.
(Ⅰ)求C;
(Ⅱ)若c=1,求△ABC的面积的最大值.
 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A.回归直线一定过样本中心( ![]() )
)
B.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
C.两个模型中残差平方和越小的模型拟合的效果越好
D.甲、乙两个模型的R2分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的两顶点为A,B如图,离心率为
的两顶点为A,B如图,离心率为 ![]() ,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.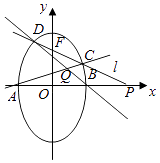
(Ⅰ)当 ![]() 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)当点P异于A,B两点时,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
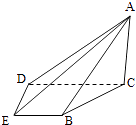
【题目】如图,在四棱锥A﹣BCDE中,平面ABC⊥平面BCDE,∠CDE=∠BED=90°,AB=CD=2,DE=BE=1,AC= ![]() .
.
(Ⅰ)证明:AC⊥平面BCDE;
(Ⅱ)求直线AE与平面ABC所成的角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,一块形状为四棱柱的木料, ![]() 分别为
分别为![]() 的中点.
的中点.
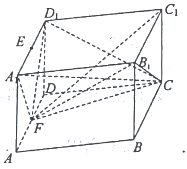
(1)要经过![]() 和
和![]() 将木料锯开,在木料上底面
将木料锯开,在木料上底面![]() 内应怎样画线?请说明理由;
内应怎样画线?请说明理由;
(2)若底面![]() 是边长为2的菱形,
是边长为2的菱形, ![]() ,
, ![]() 平面
平面![]() ,且
,且![]() ,求几何体
,求几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥E﹣ABCD中,四边形ABCD为平行四边形,△BCE为等边三角形,△ABE是以∠A为直角的等腰直角三角形,且AC=BC.
(Ⅰ)证明:平面ABE⊥平面BCE;
(Ⅱ)求二面角A﹣DE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于![]() 的函数
的函数![]() 为
为![]() 上的偶函数,且在区间
上的偶函数,且在区间![]() 上的最大值为10. 设
上的最大值为10. 设![]() .
.
⑴ 求函数![]() 的解析式;
的解析式;
⑵ 若不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
⑶ 是否存在实数![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有四个不相等的实 数根?如果存在,求出实数
有四个不相等的实 数根?如果存在,求出实数![]() 的范围,如果不存在,说明理由.
的范围,如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 年初的时候,国家政府工作报告明确提出,
年初的时候,国家政府工作报告明确提出, ![]() 年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少,
年要坚决打好蓝天保卫战,加快解决燃煤污染问题,全面实施散煤综合治理.实施煤改电工程后,某县城的近六个月的月用煤量逐渐减少, ![]() 月至
月至![]() 月的用煤量如下表所示:
月的用煤量如下表所示:
月份 |
|
|
|
|
|
|
用煤量 |
|
|
|
|
|
|
(1)由于某些原因, ![]() 中一个数据丢失,但根据
中一个数据丢失,但根据![]() 至
至![]() 月份的数据得出
月份的数据得出![]() 样本平均值是
样本平均值是![]() ,求出丢失的数据;
,求出丢失的数据;
(2)请根据![]() 至
至![]() 月份的数据,求出
月份的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)现在用(2)中得到的线性回归方程中得到的估计数据与![]() 月
月![]() 月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过
月的实际数据的误差来判断该地区的改造项目是否达到预期,若误差均不超过![]() ,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
,则认为该地区的改造已经达到预期,否则认为改造未达预期,请判断该地区的煤改电项目是否达预期?
(参考公式:线性回归方程![]() ,其中
,其中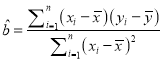
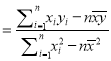 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com