
【题目】一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求
(1)连续取两次都是白球的概率;
(2)若取一个红球记2分,取一个白球记1分,取一个黑球记0分,连续取三次分数之和为4分的概率.(本小题基本事件总数较多不要求列举,但是所求事件含的基本事件要列举)
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)根据古典概型的概率求法,先列举连续取两次的基本事件总数,再找出连续取两次都是白球的基本事件的种数,然后代入公式求解.
(2)根据古典概型的概率求法,先得到连续取三次的基本事件总数,再找出连续取三次分数之和为4分的基本事件的种数,然后代入公式求解.
(1)设连续取两次的事件总数为![]() ,包括以下基本事件:
,包括以下基本事件:
(红,红),(红,白1),(红,白2),(红,黑),(白1,红)(白1,白1)(白1,白2),(白1,黑),(白2,红),(白2,白1),(白2,白2),(白2,黑),(黑,红),(黑,白1),(黑,白2),(黑,黑),故![]() 种.
种.
设事件![]() :连续取两次都是白球,包括(白1,白1),(白1,白2),(白2,白1),(白2,白2)共4个.
:连续取两次都是白球,包括(白1,白1),(白1,白2),(白2,白1),(白2,白2)共4个.
所以![]() .
.
(2)连续取三次的基本事件总数为![]() ,包括以下基本事件:
,包括以下基本事件:
(红,红,红),(红,红,白1),(红,红,白2),(红,红,黑);(红,白1,红),(红,白1,白1),……,如此,![]() 种;
种;
设事件![]() :连续取三次分数之和为4分;因为取一个红球记2分,取一个白球记1分,取一个黑球记0分,则连续取三次分数之和为4分的有如下基本事件:
:连续取三次分数之和为4分;因为取一个红球记2分,取一个白球记1分,取一个黑球记0分,则连续取三次分数之和为4分的有如下基本事件:
(红,白1,白1),(红,白1,白2),(红,白2,白1),(红,白2,白2),
(白1,红,白1),(白1,红,白2),(白2,红,白1),(白2,红,白2),
(白1,白1,红),(白1,白2,红),(白2,白1,红),(白2,白2,红),
(红,红,黑),(红,黑,红),(黑,红,红),共15个基本事件,
所以![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() ,直线
,直线![]() .
.
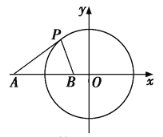
(1)求与直线l垂直,且与圆C相切的直线方程;
(2)在x轴上是否存在定点B(不同于点A),使得对于圆C上任一点P,![]() 为常数?若存在,试求这个常数值及所有满足条件的点B的坐标;若不存在,请说明理由.
为常数?若存在,试求这个常数值及所有满足条件的点B的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为()
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A.2.6天B.2.2天C.2.4天D.2.8天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn,若S9=81,a3+a5=14.
(1)求数列{an}的通项公式;
(2)设bn=![]() ,若{bn}的前n项和为Tn,证明:Tn<
,若{bn}的前n项和为Tn,证明:Tn<![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上有12个点,且任意三点不共线,以其中任意一点为始点,另一点为终点作向量,且作出所有的向量.其中3边向量的和为零向量的三角形称为“零三角形”.求以这些点为顶点的“零三角形”个数的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com