
【题目】已知函数f(x)=x22(a+2)x+a2,g(x)=x2+2(a2)xa2+8.设H1(x)=max{f(x),g(x)},H2(x)=min{f(x),g(x)}(max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值).记H1(x)的最小值为A,H2(x)的最大值为B,则AB=( )
A.a22a16B.a2+2a16
C.16D.16
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案科目:高中数学 来源: 题型:
【题目】采购经理指数(PMⅠ)是衡量一个国家制造业的“体检表”,是衡量制造业在生产、新订单、商品价格、存货、雇员、订单交货新出口订单和进口等八个方面状况的指数,图为2018年9月—2019年9月我国制造业的采购经理指数(单位:%).
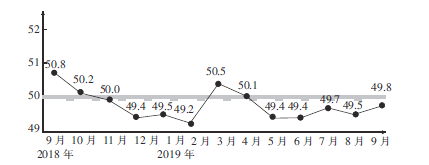
(1)求2019年前9个月我国制造业的采购经理指数的平均数(精确到0.1);
(2)从2018年10月—2019年9月这12个月任意选取4个月,记采购经理指数与上个月相比有所回升的月份个数为X,求X的分布列与期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).设
为参数).设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 变化时,
变化时,![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的普通方程;
的普通方程;
(2)设![]() 为圆
为圆![]() 上任意一点,求
上任意一点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 绕极点逆时针旋转
绕极点逆时针旋转![]() 后得到曲线
后得到曲线![]() .
.
(Ⅰ)求曲线![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() :
:![]() 与
与![]() ,
,![]() 分别相交于异于极点的
分别相交于异于极点的![]() ,
,![]() 两点,求
两点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题共l4分)
已知函数f(x)=![]() x +
x +![]() , h(x)=
, h(x)=![]() .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢宾斯基三角形是一种分形,由波兰数学家谢宾斯基在1915年提出,先作一个正三角形挖去一个“中心三角形”(即以原三角形各边的中点为顶点的三角形),然后在剩下的小三角形中又挖去一个“中心三角形”,我们用白色代表挖去的面积,那么黑三角形为剩下的面积(我们称黑三角形为谢宾斯基三角形).向图中第4个大正三角形中随机撒512粒大小均匀的细小颗粒物,则落在白色区域的细小颗粒物的数量约是( )
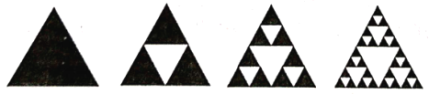
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com