
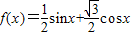 ,x∈R.
,x∈R.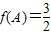 ,且
,且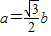 ,求角C的值.
,求角C的值.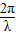 即可求出f(x)的周期,然后由x属于实数,得到这个角也属于实数,进而由正弦函数的值域[-1,1],得到函数f(x)的值域;
即可求出f(x)的周期,然后由x属于实数,得到这个角也属于实数,进而由正弦函数的值域[-1,1],得到函数f(x)的值域;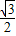 得到sin(A+
得到sin(A+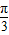 )的值,根据A的范围求出A+
)的值,根据A的范围求出A+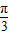 的范围,利用特殊角的三角函数值即可得到A的度数,进而求出sinA的值,由已知a与b的关系式及求出的sinA,利用正弦定理即可求出sinB的值,根据B的范围,利用特殊角的三角函数值求出B的度数,由A,B的度数,根据三角形的内角和定理求出C的度数即可.
的范围,利用特殊角的三角函数值即可得到A的度数,进而求出sinA的值,由已知a与b的关系式及求出的sinA,利用正弦定理即可求出sinB的值,根据B的范围,利用特殊角的三角函数值求出B的度数,由A,B的度数,根据三角形的内角和定理求出C的度数即可.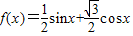 =
= ,(3分)
,(3分)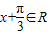 ,
,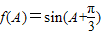 ,(6分)
,(6分)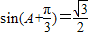 ,(7分)
,(7分)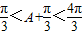 ,(8分)
,(8分)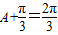 ,得到
,得到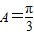 .(9分)
.(9分)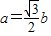 ,且
,且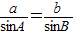 ,(10分)
,(10分)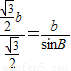 ,∴sinB=1,(11分)
,∴sinB=1,(11分)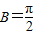 .(12分)
.(12分) .(13分)
.(13分)

科目:高中数学 来源: 题型:解答题
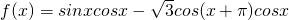 (x∈R)
(x∈R)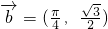 平移后得到函数y=g(x)的图象,求y=g(x)在
平移后得到函数y=g(x)的图象,求y=g(x)在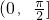 上的取值范围.
上的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省淄博一中高三(上)期中数学试卷(文科)(解析版) 题型:解答题
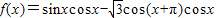 (x∈R)
(x∈R)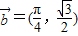 平移后得到函数y=g(x)的图象,求y=g(x)在
平移后得到函数y=g(x)的图象,求y=g(x)在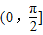 上的取值范围.
上的取值范围.查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市海淀区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
 ,x∈R.
,x∈R.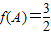 ,且
,且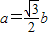 ,求角C的值.
,求角C的值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省广州市番禺区仲元中学高三(下)2月月考数学试卷(文科)(解析版) 题型:解答题
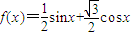 ,x∈R.
,x∈R.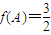 ,且
,且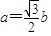 ,求角C的值.
,求角C的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com