
【题目】设函数f(x)=ex(3x﹣1)﹣ax+a,其中a<1,若有且只有一个整数x0使得f(x0)≤0,则a的取值范
围是( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:设g(x)=ex(3x﹣1),h(x)=ax﹣a,则g′(x)=ex(3x+2),
∴x∈(﹣∞,﹣ ![]() ),g′(x)<0,g(x)单调递减,
),g′(x)<0,g(x)单调递减,
x∈(﹣ ![]() ,+∞),g′(x)>0,g(x)单调递增,
,+∞),g′(x)>0,g(x)单调递增,
∴x=﹣ ![]() ,取最小值﹣3e﹣
,取最小值﹣3e﹣ ![]() ,
,
∴g(0)=﹣1<﹣a=h(0),
g(1)﹣h(1)=2e>0,
直线h(x)=ax﹣a恒过定点(1,0)且斜率为a,
∴g(﹣1)﹣h(﹣1)=﹣4e﹣1+2a≥0,
∴a≥ ![]() ,
,
a<1,
∴a的取值范围[ ![]() ,1).
,1).
故选:D.
【考点精析】通过灵活运用利用导数研究函数的单调性,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减即可以解答此题.
在这个区间单调递减即可以解答此题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】设p:实数x满足:x2﹣4ax+3a2<0(a>0),q:实数x满足:x=( ![]() )m﹣1 , m∈(1,2).
)m﹣1 , m∈(1,2).
(1)若a= ![]() ,且p∧q为真,求实数x的取值范围;
,且p∧q为真,求实数x的取值范围;
(2)q是p的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点 ![]() 与定点
与定点 ![]() 的距离和它到定直线
的距离和它到定直线 ![]() 的距离的比是
的距离的比是 ![]() ∶
∶ ![]() ,记点
,记点 ![]() 的轨迹为
的轨迹为 ![]() .
.
(1)求曲线 ![]() 的方程;
的方程;
(2)对于定点 ![]() ,作过点
,作过点 ![]() 的直线
的直线 ![]() 与曲线
与曲线 ![]() 交于不同的两点
交于不同的两点 ![]() ,
, ![]() ,求△
,求△ ![]() 的内切圆半径的最大值.
的内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有10个不同的产品,其中4个次品,6个正品.现每次取其中一个进行测试,直到4个次品全测完为止,若最后一个次品恰好在第五次测试时被发现,则该情况出现的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知直线l:x+ ![]() y﹣c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
y﹣c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜. 
(1)如果走私船和巡逻船相距6海里,求走私船能被截获的点的轨迹;
(2)若O与公海的最近距离20海里,要保证在领海内捕获走私船(即不能截获走私船的区域与公海不想交).则O,A之间的最远距离是多少海里?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC, 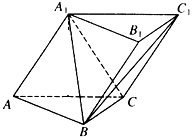
(Ⅰ)求证:AC⊥A1B;
(Ⅱ)求二面角A﹣A1C﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆的方程为x2+y2﹣6x=0,过点(1,2)的该圆的三条弦的长a1 , a2 , a3构成等差数列,则数列a1 , a2 , a3的公差的最大值是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)若y=f(x)在(0,+∞)恒单调递减,求a的取值范围;
(2)若函数y=f(x)有两个极值点x1 , x2(x1<x2),求a的取值范围并证明x1+x2>2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,横、纵坐标均为整数的点叫做格点.若函数y=f(x)的图象恰好经过k个格点,则称函数y=f(x)为k阶格点函数.已知函数:①y=x2;②y=2sinx,③y=πx﹣1;④y=cos(x+ ![]() ).其中为一阶格点函数的序号为(注:把你认为正确论断的序号都填上)
).其中为一阶格点函数的序号为(注:把你认为正确论断的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com