练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法中正确的是（ ）

    A.先把高二年级的2000名学生编号：1到2000，再从编号为1到50的学生中随机抽取1名学生，其编号为，然后抽取编号为，，，…的学生，这种抽样方法是分层抽样法

    B.线性回归直线不一定过样本中心

    C.若一个回归直线方程为，则变量每增加一个单位时，平均增加3个单位

    D.若一组数据2，4，，8的平均数是5，则该组数据的方差也是5

    【答案】D

    【解析】

    根据系统抽样，样本中心点，回归直线，平均数，方差，对各选项逐一判断即可.

    对于A：根据个体数目较多，且没有明显的差异，抽取样本间隔相等，知这种抽样方法是系统抽样法，故A错误；

    对于B：线性回归直线一定过样本中心，故B错误；

    对于C：对回归直线，当变量每增加一个单位时，平均减少3个单位，故C错误；

    对于D：一组数据2，4，，8的平均数是5，则，即，

    所以该组数据的方差为，故D正确.

    故选：D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等.如图是源于其思想的一个程序框图，若输入，，则输出的等于（ ）

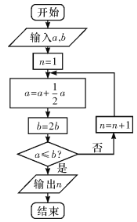
    A. 3B. 4C. 5D. 6

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）若，求的取值范围；

    （2）若，的图像与轴围成的封闭图形面积为，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知m是实数，关于x的方程E：x2﹣mx+（2m+1）＝0．

    （1）若m＝2，求方程E在复数范围内的解；

    （2）若方程E有两个虚数根x1，x2，且满足|x1﹣x2|＝2，求m的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设抛物线Γ的方程为y2＝4x，点P的坐标为（1，1）．

    （1）过点P，斜率为﹣1的直线l交抛物线Γ于U，V两点，求线段UV的长；

    （2）设Q是抛物线Γ上的动点，R是线段PQ上的一点，满足2，求动点R的轨迹方程；

    （3）设AB，CD是抛物线Γ的两条经过点P的动弦，满足AB⊥CD．点M，N分别是弦AB与CD的中点，是否存在一个定点T，使得M，N，T三点总是共线？若存在，求出点T的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥PABCD的底面ABCD是矩形，PA⊥底面ABCD，点E、F分别是棱PC、PD的中点，则

    ①棱AB与PD所在直线垂直；

    ②平面PBC与平面ABCD垂直；

    ③△PCD的面积大于△PAB的面积；

    ④直线AE与直线BF是异面直线．

    以上结论正确的是________．(写出所有正确结论的序号)

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆的左、右焦点分别为，右顶点为A，上顶点为B，且满足向量 。

    （1）若，求椭圆的标准方程;

    （2）设为椭圆上异于顶点的点，以线段PB为直径的圆经过F1，问是否存在过F2的直线与该圆相切？若存在，求出其斜率；若不存在，说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，对任意，都有.

    讨论的单调性；

    当存在三个不同的零点时，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为实数常数）

    （1）当时，求函数在上的单调区间；

    （2）当时，成立，求证：．

    查看答案和解析>>

    同步练习册答案