
【题目】2014年,中央和国务院办公厅印发《关于引导农村土地经营权有序流转发展农业适度规模经营的意见》,要求大力发展土地流转和适度规模经营.某种粮大户2015年开始承包了一地区的大规模水田种植水稻,购买了一种水稻收割机若干台,这种水稻收割机随着使用年限的增加,每年的养护费也相应增加,这批水稻收割机自购买使用之日起,5年以来平均每台水稻收割机的养护费用数据统计如下:
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
养护费用 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
(1)从这5年中随机抽取2年,求平均每台水稻收割机每年的养护费用至少有1年多于2万元的概率;
(2)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)若该水稻收割机的购买价格是每台16万元,由(2)中的回归方程,从每台水稻收割机的年平均费用角度,你认为一台该水稻收割机是使用满5年就淘汰,还是继续使用到满8年再淘汰?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: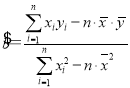 ,
,![]()
![]() .
.
【答案】(1)0.7;(2)![]() ;(3)建议使用到满8年再淘汰
;(3)建议使用到满8年再淘汰
【解析】
(1)利用古典概型判断即可;
(2)根据线性回归方程公式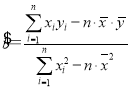 ,求出
,求出![]() ,代入求出
,代入求出![]() ,求出线性回归方程;
,求出线性回归方程;
(3)根据(2)线性回归方程,估算满5年和满8年的平均费用,判断即可.
(1)根据题意,从这5年中随机抽取2年,每台水稻收割机每年的养护费所有可能的结果有10种,
![]() ,
,![]() ,
,![]() ,
,
其中2年的养护费用不多于2万元的有3种,![]() ,
,
故所求概率为![]() ;
;
(2)根据表格的![]() ,
,![]() ,
,
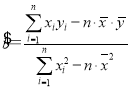 =
=![]() ,
,
![]()
![]() ,
,
故线性回归方程为![]() ;
;
(3)若满5年就淘汰,则每台水稻收割机年平均费用为![]() (万元),
(万元),
若满8年淘汰,则每台水稻收割机的年平均费用为![]() (万元),
(万元),
所以使用满8年的年平均费用低于使用满5年的年平均费用,
建议使用到满8年再淘汰.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】近年来,随着“雾霾”天出现的越来越频繁,很多人为了自己的健康,外出时选择戴口罩,长郡中学高三兴趣研究小组利用暑假空闲期间做了一项对人们雾霾天外出时是否戴口罩的调查,共调查了120人,其中女性70人,男性50人,并根据统计数据画出等高条形图如图所示:
(Ⅰ)利用图形判断性别与雾霾天外出戴口罩是否有关系;
(Ⅱ)根据统计数据建立一个![]() 列联表;
列联表;
(Ⅲ)能否在犯错误的概率不超过0.05的前提下认为性别与雾霾天外出戴口罩有关系.
附: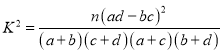

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扇形AOB中心角为![]() ,所在圆半径为
,所在圆半径为![]() ,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.

(1)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设![]() ;
;
(2)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设![]() ;
;
试研究(1)(2)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:

根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:①函数![]() ;
;
②向量![]() ,
,![]() ,且
,且![]() ,
,![]() ;
;
③函数![]() 的图象经过点
的图象经过点![]()
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知_________________,且函数![]() 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 在
在![]() 上的单调递减区间.
上的单调递减区间.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国剩余定理”又称“孙子定理”.1852年,英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.“中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将1到2019这2019个数中,能被3除余2且被5整除余2的数按从小到大的顺序排成一列,构成数列![]() ,则此数列所有项中,中间项的值为( )
,则此数列所有项中,中间项的值为( )
A.992B.1022C.1007D.1037
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台O1O2的轴截面为等腰梯形A1A2B2B1,A1A2![]() B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
B1B2,A1A2=2B1B2,A1B1=2,圆台O1O2的侧面积为6π.若点C,D分别为圆O1,O2上的动点且点C,D在平面A1A2B2B1的同侧.
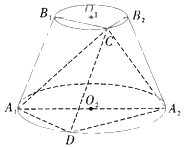
(1)求证:A1C⊥A2C;
(2)若∠B1B2C=60°,则当三棱锥C﹣A1DA2的体积取最大值时,求A1D与平面CA1A2所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节(每年农历五月初五),是中国传统节日,有吃粽子的习俗.某超市在端午节这一天,每售出![]() kg粽子获利润
kg粽子获利润![]() 元,未售出的粽子每
元,未售出的粽子每![]() kg亏损
kg亏损![]() 元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了
元.根据历史资料,得到销售情况与市场需求量的频率分布表,如下表所示.该超市为今年的端午节预购进了![]() kg粽子.以
kg粽子.以![]() (单位:kg,
(单位:kg,![]() )表示今年的市场需求量,
)表示今年的市场需求量,![]() (单位:元)表示今年的利润.
(单位:元)表示今年的利润.
市场需求量(kg) |
|
|
|
|
|
频率 | 0.1 | 0.2 | 0.3 | 0.25 | 0.15 |
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据频率分布表估计今年利润![]() 不少于
不少于![]() 元的概率.
元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com