设an是关于x的方程xn+nx-1=0(n∈N*,x∈(0,+∞))的根.试证明:
(1)an∈(0,1);
(2)an+1<an;
(3)a12+a22+…+an2<1.
证明:(1)设f(x)=x
n+nx-1,
∵f(0)=-1<0,f(1)=n>0,
且函数f(x)的图象在(0,+∞)上是连续的,
∴f(x)在(0,1)上至少有一个零点,
即方程x
n+nx-1=0在(0,1)内至少有一个根.
∵x∈(0,+∞),
∴f′(x)=nx
n-1+n>0,
∴f(x)在(0,+∞)上是增函数.
∴方程x
n+nx-1=0在(0,+∞)内有唯一根,
且根在(0,1)内,即a
n∈(0,1).
(2)方法一:∵
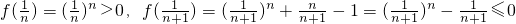
,
且函数f(x)的图象在(0,+∞)上是连续的,
∴f(x)在
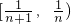
内至少有一个零点,
即方程x
n+nx-1=0在
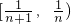
内至少有一个根.
又由(1)知函数f(x)在(0,+∞)上单调递增,
∴方程x
n+nx-1=0在
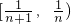
内有唯一根,
∴
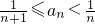
.
∴
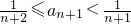
,
∴a
n+1<a
n.
方法二:由(1)知,a
nn+na
n-1=0,
a
n+1n+1+(n+1)a
n+1-1=0,
两式相减得:a
n+1n+1+(n+1)a
n+1-a
nn-na
n=0,
若存在n∈N
*,使得a
n+1≥a
n,
则a
n+1≥a
n>a
nn,
从而a
n+1n+1+(n+1)a
n+1-a
nn-na
n>(n+1)a
n+1-a
nn-na
n=a
n+1-a
nn+na
n+1-na
n>0,矛盾.
所以a
n+1<a
n.
(3)由题设得

,
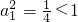
,
当n∈N
*时,

.
∴
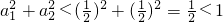
.
当n≥3时有a
12+a
22+a
32+…
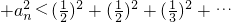
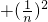
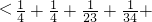
…
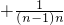
=
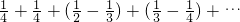
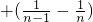
=
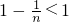
.
综上a
12+a
22+…+a
n2<1.
分析:(1)设f(x)=x
n+nx-1,由f(0)=-1<0,f(1)=n>0,且函数f(x)的图象在(0,+∞)上是连续的,知f(x)在(0,1)上至少有一个零点,即方程x
n+nx-1=0在(0,1)内至少有一个根,由此能够证明a
n∈(0,1).
(2)法一:由
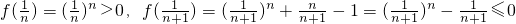
,且函数f(x)的图象在(0,+∞)上是连续的,知f(x)在
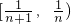
内至少有一个零点,由函数f(x)在(0,+∞)上单调递增,知方程x
n+nx-1=0在
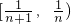
内有唯一根,由此能证明a
n+1<a
n. (9分)
法二:由a
nn+na
n-1=0,a
n+1n+1+(n+1)a
n+1-1=0,得:a
n+1n+1+(n+1)a
n+1-a
nn-na
n=0,由此利用反证法能够证明a
n+1<a
n.
(3)由题设得

,
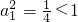
,当n∈N
*时,

.故
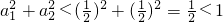
.由此能够证明a
12+a
22+…+a
n2<1.
点评:本题考查数列与不等式的综合运用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,计算繁琐,易出错,是高考的重点.解题时要认真审题,注意反证明法的灵活运用,仔细解答,注意培养计算能力.

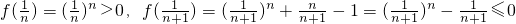 ,
,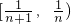 内至少有一个零点,
内至少有一个零点,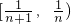 内至少有一个根.
内至少有一个根.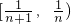 内有唯一根,
内有唯一根,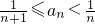 .
.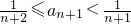 ,
, ,
,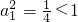 ,
, .
.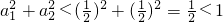 .
. 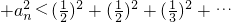
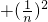
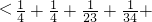 …
…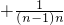
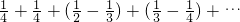
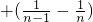
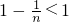 .
.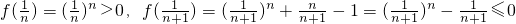 ,且函数f(x)的图象在(0,+∞)上是连续的,知f(x)在
,且函数f(x)的图象在(0,+∞)上是连续的,知f(x)在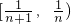 内至少有一个零点,由函数f(x)在(0,+∞)上单调递增,知方程xn+nx-1=0在
内至少有一个零点,由函数f(x)在(0,+∞)上单调递增,知方程xn+nx-1=0在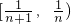 内有唯一根,由此能证明an+1<an. (9分)
内有唯一根,由此能证明an+1<an. (9分) ,
,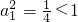 ,当n∈N*时,
,当n∈N*时, .故
.故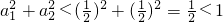 .由此能够证明a12+a22+…+an2<1.
.由此能够证明a12+a22+…+an2<1.

 备战中考寒假系列答案
备战中考寒假系列答案