
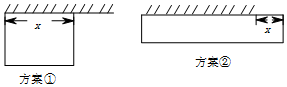
 �Ϻ��и��˸���ѧ���ڸ�����������2015��9����ʽ��ʼ������ҪΧ��һ�������900ƽ���ľ��εس��ص�Χǽ����һ�泤��Ϊ20�ľ�ǽ��ͼ��б�ܲ������мס�������ά�����þ�ǽ������
�Ϻ��и��˸���ѧ���ڸ�����������2015��9����ʽ��ʼ������ҪΧ��һ�������900ƽ���ľ��εس��ص�Χǽ����һ�泤��Ϊ20�ľ�ǽ��ͼ��б�ܲ������мס�������ά�����þ�ǽ���������� ��1����ѡȡx�׳��ľ�ǽ����þ��ε���һ��Ϊ$\frac{900}{x}$�ף������⣬�ɵ�������y1=10x+80x+$\frac{2��900��80}{x}$�����������õĵ����ԣ��ɵ���Сֵ��
��2���迿��ǽ��һ�߳�Ϊx�ף����о�ǽΪa�ף���þ��ε���һ��Ϊ$\frac{900}{x}$�ף������⣬�ɵ�������y2=200+80��x-20��+80x+$\frac{2��900��80}{x}$��
��3��y1=10x+80x+$\frac{2��900��80}{x}$�����������õĵ����ԣ��ɵ���Сֵ��y2=200+80��x-20��+80x+$\frac{2��900��80}{x}$�����������û�������ʽ�ɵ���Сֵ�������жϣ�
��� �⣺��1����ѡȡx�׳��ľ�ǽ������ε���һ��Ϊ$\frac{900}{x}$�ף�
�����⣬�ɵ�������y1=10x+80x+$\frac{2��900��80}{x}$
=90��x+$\frac{1600}{x}$����0��x��20����
��2���迿��ǽ��һ�߳�Ϊx�ף����о�ǽΪ20�ף�����ε���һ��Ϊ$\frac{900}{x}$�ף�
�����⣬�ɵ�������y2=200+80��x-20��+80x+$\frac{2��900��80}{x}$
=160��x+$\frac{900}{x}$��-1400����x��20����
��3����y=x+$\frac{1600}{x}$�ڣ�0��20]�ݼ����ɵ�y1����СֵΪ9000Ԫ���ɵ�x=30��y2����СֵΪ8200Ԫ��
��y1��y2�����ҷ������ã�
���� ���⿼���������ʽ����ֵ�����е����ã�����Ĺؼ�����ȷ���⣬�����������ú����Ľ���ʽ�������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=cosx | B�� | y=sinx | C�� | y=tanx | D�� | y=ex |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com