
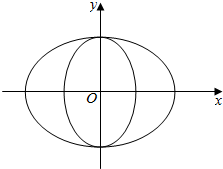
 ��ͼ�����ߦ���������ԲT1��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$����ԲT2��$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1��{b��c��0}��$��ɣ���a��b��c�ɵȱ�����ʱ�������ߦ�Ϊ��è�����ߡ���
��ͼ�����ߦ���������ԲT1��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$����ԲT2��$\frac{y^2}{b^2}+\frac{x^2}{c^2}=1��{b��c��0}��$��ɣ���a��b��c�ɵȱ�����ʱ�������ߦ�Ϊ��è�����ߡ������� ��1��������֪$b=\sqrt{2}$��$\frac{b}{a}$=$\frac{c}{b}$=$\frac{\sqrt{2}}{2}$���Ӷ���è�����ߦ��ķ��̣�
��2���轻��C��x1��y1����D��x2��y2�����Ӷ��ɵ�${x_0}=\frac{{{x_1}+{x_2}}}{2}��{y_0}=\frac{{{y_1}+{y_2}}}{2}$���������̻���ɵ�$k•{k_{OM}}=-\frac{1}{2}$��k•kON=-2���Ӷ���ã�
��3����ֱ��l�ķ���Ϊ$y=\sqrt{2}x+m$���������̻���$��{{b^2}+2{c^2}}��{x^2}+2\sqrt{2}m{c^2}x+{m^2}{c^2}-{b^2}{c^2}=0$���Ӷ��ɵ�${l_1}��y=\sqrt{2}x+\sqrt{{b^2}+2{c^2}}$��ͬ���ɵ�${l_2}��y=\sqrt{2}x-\sqrt{{b^2}+2{a^2}}$���Ӷ�������ƽ��������ʾ�����εĸߣ�����$|{AB}|=\frac{{2\sqrt{3}ab\sqrt{2{a^2}-2{c^2}}}}{{{b^2}+2{a^2}}}$���Ӷ�����������
��� �⣺��1��������֪��$b=\sqrt{2}$��$\frac{b}{a}$=$\frac{c}{b}$=$\frac{\sqrt{2}}{2}$��
��a=2��c=1��
��${T_1}��\frac{x^2}{4}+\frac{y^2}{2}=1$����${T_2}��\frac{y^2}{2}+{x^2}=1$��
��2��֤������б��Ϊk��ֱ�߽���ԲT1�ڵ�C��x1��y1����D��x2��y2�����߶�CD�е�M��x0��y0����
��${x_0}=\frac{{{x_1}+{x_2}}}{2}��{y_0}=\frac{{{y_1}+{y_2}}}{2}$��
��$\left\{\begin{array}{l}\frac{{{x_1}^2}}{4}+\frac{{{y_1}^2}}{2}=1\\ \frac{{{x_2}^2}}{4}+\frac{{{y_2}^2}}{2}=1\end{array}\right.$��$\frac{{��{{x_1}-{x_2}}����{{x_1}+{x_2}}��}}{4}+\frac{{��{{y_1}-{y_2}}����{{y_1}+{y_2}}��}}{2}=0$��
��k������k��0��
��x1��x2����x0��0��
��$\frac{{{y_1}-{y_2}}}{{{x_1}-{x_2}}}•\frac{y_0}{x_0}=-\frac{1}{2}$��
��$k•{k_{OM}}=-\frac{1}{2}$��
ͬ����k•kON=-2��
��$\frac{{{k_{OM}}}}{{{k_{ON}}}}=\frac{1}{4}$��
��3����ֱ��l�ķ���Ϊ$y=\sqrt{2}x+m$��
�������̵�$\left\{\begin{array}{l}y=\sqrt{2}x+m\\ \frac{y^2}{b^2}+\frac{x^2}{c^2}=1\end{array}\right.$��
����ã�$��{{b^2}+2{c^2}}��{x^2}+2\sqrt{2}m{c^2}x+{m^2}{c^2}-{b^2}{c^2}=0$��
�ɡ�=0�����m2=b2+2c2��
${l_1}��y=\sqrt{2}x+\sqrt{{b^2}+2{c^2}}$��
�������̵�$\left\{\begin{array}{l}y=\sqrt{2}x+m\\ \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{array}\right.$��
�����$��{{b^2}+2{a^2}}��{x^2}+2\sqrt{2}m{a^2}x+{m^2}{a^2}-{b^2}{a^2}=0$��
�ɡ�=0��m2=b2+2a2��
${l_2}��y=\sqrt{2}x-\sqrt{{b^2}+2{a^2}}$��
��ƽ������룺$d=\frac{{\sqrt{{b^2}+2{c^2}}+\sqrt{{b^2}+2{a^2}}}}{{\sqrt{3}}}$��
��$|{AB}|=\frac{{2\sqrt{3}ab\sqrt{2{a^2}-2{c^2}}}}{{{b^2}+2{a^2}}}$��
���ABN��������ֵΪ$S=\frac{1}{2}|{AB}|•d=\frac{{ab\sqrt{2{a^2}-2{c^2}}��{\sqrt{{b^2}+2{c^2}}+\sqrt{{b^2}+2{a^2}}}��}}{{{b^2}+2{a^2}}}$��
���� ���⿼����ѧ���Ļ����������������Բ��ֱ�ߵ�λ�ù�ϵ���ж���Ӧ�ã�


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ij�����꼶�Ӽף��ģ��ң����������꼶���ѡ��7��ѧ���μӸ�У����������ѧѡ�ο��ԣ�����ȡ�õijɼ������֣�100�֣��ľ�Ҷͼ��ͼ��ʾ�����м���ѧ����ƽ������85�֣�����ѧ���ɼ�����λ����83�֣�
ij�����꼶�Ӽף��ģ��ң����������꼶���ѡ��7��ѧ���μӸ�У����������ѧѡ�ο��ԣ�����ȡ�õijɼ������֣�100�֣��ľ�Ҷͼ��ͼ��ʾ�����м���ѧ����ƽ������85�֣�����ѧ���ɼ�����λ����83�֣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2��+�ޣ� | B�� | ��0��2�� | C�� | ��0��4�� | D�� | ��4��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
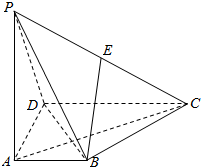 ��ͼ��������P-ABCD�У�PA��ABCD��AD��AB��AB��DC��AD=DC=AP=2��AB=1����EΪ��PC���е㣮
��ͼ��������P-ABCD�У�PA��ABCD��AD��AB��AB��DC��AD=DC=AP=2��AB=1����EΪ��PC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com