
【题目】已知函数 ,记不等式f(x)≤4的解集为M,记函数
,记不等式f(x)≤4的解集为M,记函数![]() 的定义域为集合N.
的定义域为集合N.
(Ⅰ)求集合M和N;
(Ⅱ)求M∩N和M∪(RN).
【答案】(1){x|﹣![]() ≤x≤3}; (2){x|x≤1或x>3}.
≤x≤3}; (2){x|x≤1或x>3}.
【解析】
Ⅰ)利用分类讨论法求出f(x)≤4的解集M和g(x)的定义域N;
(Ⅱ)根据集合的运算法则求出M∩N和M∪RN的值.
函数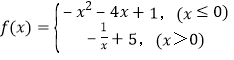 ,
,
当x≤0时,f(x)=﹣x2﹣4x+1≤4,即x2+4x+3≥0,
解得x≤﹣3或﹣1≤x≤0,
当x>0时,f(x)=﹣![]() +5≤4,解得0<x≤1;
+5≤4,解得0<x≤1;
综上,不等式f(x)≤4的解集M={x|x≤﹣3或﹣1≤x≤1};
∵函数g(x)=![]() 的定义域为集合N,
的定义域为集合N,
∴N={x|﹣2x2+5x+3≥0}={x|﹣![]() ≤x≤3};
≤x≤3};
(Ⅱ)由题意知,M∩N={x|﹣![]() ≤x≤1},
≤x≤1},
RN={x|x<﹣![]() 或x>3},
或x>3},
∴M∪RN={x|x≤1或x>3}.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)是定义域为R的偶函数. 当x≥0时,f(x)= 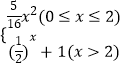 ,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是 .
,若关于x的方程[f(x)]2+af(x)+b=0,a,b∈R有且仅有6个不同实数根,则实数a的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直三棱柱![]() 中,底面
中,底面![]() 是边长为2的正三角形,
是边长为2的正三角形, ![]() 是棱
是棱![]() 的中点,且
的中点,且![]() .
.
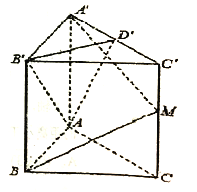
(1)若点![]() 为棱
为棱![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(2)若点![]() 在棱
在棱![]() 上,且
上,且![]() 平面
平面![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)判断函数![]() 在
在![]() 的单调性.(不需要证明);
的单调性.(不需要证明);
(2)探究是否存在实数![]() ,使得函数
,使得函数![]() 为奇函数?若存在,求出
为奇函数?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)在(2)的条件下,解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点与抛物线
的右焦点与抛物线![]() 的焦点重合,且该椭圆的离心率与双曲线
的焦点重合,且该椭圆的离心率与双曲线![]() 的离心率互为倒数.
的离心率互为倒数.
(1)求椭圆的方程;
(2)设直线![]() 与椭圆相交于不同的两点
与椭圆相交于不同的两点![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且
的垂直平分线上,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]()
(1)设![]() ,
,![]() ,若函数
,若函数![]() 存在零点,求a的取值范围;
存在零点,求a的取值范围;
(2)若![]() 是偶函数,求
是偶函数,求![]() 的值;
的值;
(3)在(2)条件下,设![]() ,若函数
,若函数![]() 与
与![]() 的图象只有一个公共点,求实数b的取值范围.
的图象只有一个公共点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四边形BFED是以BD为直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD. (Ⅰ)求证:AD⊥平面BFED;
(Ⅱ)在线段EF上是否存在一点P,使得平面PAB与平面ADE所成的锐二面角的余弦值为 ![]() .若存在,求出点P的位置;若不存在,说明理由.
.若存在,求出点P的位置;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com