
【题目】已知函数f(x)=(x2+ax+a)e﹣x , (a为常数,e为自然对数的底).
(1)当a=0时,求f′(2);
(2)若f(x)在x=0时取得极小值,试确定a的取值范围;
(3)在(2)的条件下,设由f(x)的极大值构成的函数为g(a),将a换元为x,试判断曲线y=g(x)是否能与直线3x﹣2y+m=0(m为确定的常数)相切,并说明理由.
【答案】
(1)解:(1)当a=0时,f(x)=x2e﹣x,f'(x)=2xe﹣x﹣x2e﹣x=xe﹣x(2﹣x).
所以f'(2)=0.
(2)解:f'(x)=(2x+a)e﹣x﹣e﹣x(x2+ax+a)=e﹣x[﹣x2+(2﹣a)x]=﹣e﹣xx[x﹣(2﹣a)].
令f'(x)=0,得x=0或x=2﹣a.
若2﹣a=0,即a=2时,f'(x)=﹣x2e﹣x≤0恒成立,
此时f(x)在区间(﹣∞,+∞)上单调递减,没有极小值;
当2﹣a>0,即a<2时,
若x<0,则f'(x)<0.
若0<x<2﹣a,则f'(x)>0.
所以x=0是函数f(x)的极小值点.
当2﹣a<0,即a>2时,
若x>0,则f'(x)<0.
若2﹣a<x<0,则f'(x)>0.
此时x=0是函数f(x)的极大值点.
综上所述,使函数f(x)在x=0时取得极小值的a的取值范围是a<2.
(3)解:由(2)知当a<2,且x>2﹣a时,f'(x)<0,
因此x=2﹣a是f(x)的极大值点,极大值为f(2﹣a)=(4﹣a)ea﹣2.
所以g(x)=(4﹣x)ex﹣2(x<2).
g'(x)=﹣ex﹣2+ex﹣2(4﹣x)=(3﹣x)ex﹣2.
令h(x)=(3﹣x)ex﹣2(x<2).
则h'(x)=(2﹣x)ex﹣2>0恒成立,即h(x)在区间(﹣∞,2)上是增函数.
所以当x<2时,h(x)<h(2)=(3﹣2)e2﹣2=1,即恒有g'(x)<1.
又直线3x﹣2y+m=0的斜率为 ![]() ,
,
所以曲线y=g(x)不能与直线3x﹣2y+m=0相切.
【解析】(1)把a=0代入函数解析式,求导后直接把x=2代入导函数解析式计算(2)求出原函数的导函数,解出导函数的零点为0或2﹣a,分2﹣a=0、2﹣a>0、2﹣a<0三种情况讨论导函数在不同区间内的符号,判出极小值点,从而得到使f(x)在x=0时取得极小值的a的取值范围;(3)由(2)中的条件,能够得到x=2﹣a是f(x)的极大值点,求出f(2﹣a),得到g(x),两次求导得到函数g(x)的导数值小于1,而直线3x﹣2y+m=0的斜率为 ![]() ,说明曲线y=g(x)与直线3x﹣2y+m=0不可能相切.
,说明曲线y=g(x)与直线3x﹣2y+m=0不可能相切.


科目:高中数学 来源: 题型:
【题目】已知{an}是等比数列,an>0,a3=12,且a2,a4,a2+36成等差数列.
(1)求数列{an}的通项公式;
(2)设{bn}是等差数列,且b3=a3,b9=a5,求b3+b5+b7+…+b2n+1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知直线2x﹣y﹣4=0与直线x﹣2y+1=0交于点p.
(1)求过点p且垂直于直线3x+4y﹣15=0的直线l1的方程;(结果写成直线方程的一般式)
(2)求过点P并且在两坐标轴上截距相等的直线l2方程(结果写成直线方程的一般式)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)=3sin(2x+φ)的图象关于点( ![]() ,0)成中心对称(|φ|<
,0)成中心对称(|φ|< ![]() ),那么函数f(x)图象的一条对称轴是( )
),那么函数f(x)图象的一条对称轴是( )
A.x=﹣ ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知如表为“五点法”绘制函数f(x)=Asin(ωx+φ)图象时的五个关键点的坐标(其中A>0,ω>0,|φ|<π)
x | ﹣ |
|
|
|
|
f(x) | 0 | 2 | 0 | ﹣2 | 0 |
(Ⅰ)请写出函数f(x)的最小正周期和解析式;
(Ⅱ)求函数f(x)的单调递减区间;
(Ⅲ)求函数f(x)在区间[0, ![]() ]上的取值范围.
]上的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图的程序框图表示的算法中,输入三个实数a,b,c,要求输出的x是这三个数中最大的数,那么在空白的判断框中,应该填入( ) 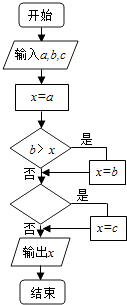
A.x>c
B.c>x
C.c>b
D.c>a
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=﹣ ![]() x3+x2+(m2﹣1)x,(x∈R),其中m>0.
x3+x2+(m2﹣1)x,(x∈R),其中m>0.
(1)当m=1时,曲线y=f(x)在点(1,f(1))处的切线斜率;
(2)求函数的单调区间与极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com